|
Томографическая диагностика нелинейных сред Томский государственный университет Научный руководитель: Якубов Владимир Петрович, доктор физ.-мат. наук В настоящее время существует множество томографических подходов, основанных на учете различных эффектов взаимодействия излучения с веществом. Данные методы используют предположение о линейности исследуемой среды, т.е. отсутствии зависимости параметров среды от характеристик излучения. Однако существующие методы не дают достаточной информации об исследуемой среде. Поэтому предпринимаются попытки создания альтернативных методов томографии, обладающих новыми возможностями за счет учета нелинейных эффектов. В частности, исследования влияния микроволнового излучения на биологические системы показали, что биоклетка представляет собой нелинейную среду уже при малых интенсивностях излучения. Поскольку большинство заболеваний связаны с изменениями на клеточном уровне, то определение нелинейных свойств тканей будет способствовать более точной диагностике и лечению заболеваний. Несмотря на перспективность таких задач, существующие методы анализа поля в нелинейной среде развиты слабо, что не дает возможности создания эффективных методов томографической диагностики нелинейных сред. Задача томографии нелинейных сред состоит в определении пространственной структуры исследуемой среды и нахождении нелинейной характеристики в каждой ее точке. Для ее решения необходимо сначала решить прямую задачу определения полного поля, испытавшего взаимодействие с исследуемой средой. Выделим в диэлектрической проницаемости линейную и нелинейную части следующим образом:
где линейная составляющая
Здесь Для решения обратной задачи необходимо сначала восстановить плотность вторичных источников среды в зависимости от пространственной координаты. Пусть объем сканируется антенной с d -диаграммой направленности по координате z в целиндрической системе координат:
где
Это преобразование является обобщением известных томографических решений. Для получения искомой пространственно-временной нелинейной характеристики среды необходимо знать полное поле в каждой точке среды. Его можно определить в результате подстановки найденного распределения вторичных источников в (2). Для определения нелинейных свойств диэлектрической проницаемости и проводимости необходимо определить спектр этих величин, а затем, используя обратное преобразование Фурье, найти их зависимость от пространственных координат, времени, и величины воздействующего поля. Результаты, полученные в работе, позволяют подойти к решению проблемы диагностики и томографии нелинейных неоднородных сред, что позволит повысить точность и оперативность получения информации об объекте в самых различных областях применения. Работа поддержана грантом Минобразования Т00-2.4-2119. [1] Якубов В.П., Лосев Д.В., Мальцев А.И. Диагностика нелинейностей по возмущениям рассеянного поля// Известия вузов. Радиофизика. - 2000. - Т. 43, № 7. - С. 645-651. |
| (c) АСФ России, 2001 |
 ,(3)
,(3)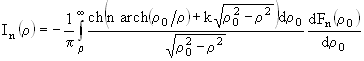 (4)
(4)