|
Релаксация диэлектрической проницаемости в кристаллах триглицинсульфата (ТГС) при изменении температуры Тверской государственный университет Научный руководитель: Иванов Владимир Васильевич, кандидат физ.-мат. наук Под воздействием температуры в сегнетоэлектрическом кристалле происходит изменение во времени различных физических величин, в том числе и диэлектрической проницаемости e .Установлено, что экспериментально полученные временные зависимости диэлектрической проницаемости e хорошо описываются эмпирическим законом:
где t и a - параметры (a i 1).Или в самом общем виде это можно представить как:
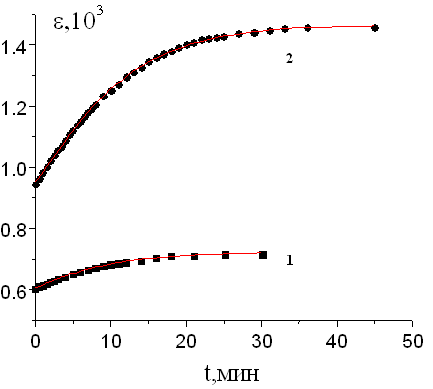
где e о и e ? - начальное и конечное значение диэлектрической проницаемости соответственно.При изменении температуры сегнетоэлектрического кристалла и воздействии внешнего электрического поля происходит нарушение его термодинамического равновесия. Благодаря дефектной структуре реальных кристаллов высоты потенциальных барьеров, которые преодолевает доменная стенка при ее движении к новому энергетически выгодному состоянию, неодинаковы. Следовательно, является целесообразным представление о целом спектре времен релаксации. Параметр a является характеристикой распределения времен релаксации: при a =1 - одно время релаксации, чем сильнее a отличается от единицы, тем шире будет спектр времен релаксации. В результате обработки экспериментальных данных установлено, что по мере удаления от точки Кюри в низкотемпературную область параметр a стремится к R 1, т.е. спектр времен релаксации сужается, а значение параметра t , являющегося средним временем релаксации, уменьшается (рис.1a). Сплошная линия - график функции f ~ exp(-(t/t )a ), аппроксимирующей экспериментальные данные.При уменьшении скачка температуры D Т ход временной зависимости диэлектрической проницаемости не изменяется, однако численные значения параметров a и t не остаются постоянными и зависят от величины скачка D Т.Для выборочных значений параметра a № 1 были построены графики функций распределения времен релаксации G(t ).Для нахождения функции распределения необходимо решить интегральное уравнение Фредгольма первого рода:
Искомая функция G(t ):
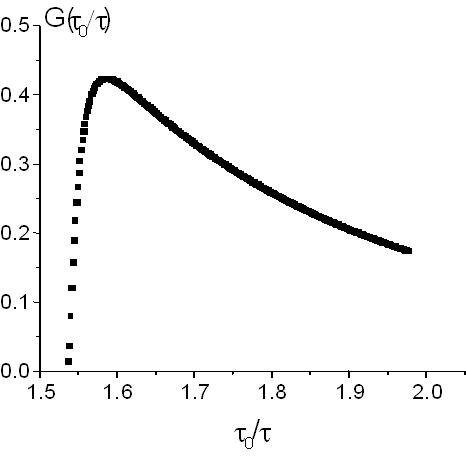
На рис.1b представлена характерная функция распределения при a = 1.2.
Рис.1 (a,b) Рис.1a - Временные зависимости диэлектрической проницаемости: 1 - D T1: 200 С R 300 C, параметр a = 1.1, t =9 мин.; 2 - D T2: 300 СR 400 C, параметр a =1.2, t = 11 мин. Рис.1b - Вид функции-оригинала преобразования Лапласа при a =1.2 |
| (c) АСФ России, 2001 |
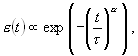 (1)
(1)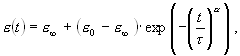 (2)
(2)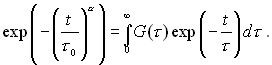 (3)
(3) (4)
(4)