|
Исследование катафореза в импульсно-периодическом разряде He-Sr рекомбинационного лазера Ростовский государственный университет Научный руководитель: Чеботарев Геннадий Дмитриевич; Латуш Евгений Леонидович, кандидат физико-математических наук; кандидат физико-математических наук Явление катафореза успешно применяется в непрерывных лазерах на парах металлов (ЛПМ) для ввода паров в активную среду. В работе [1] было предложено использовать катафорезный ввод паров в импульсно-периодических ЛПМ и впервые экспериментально получена генерация в импульсных He-Cd (λ =533,7 θ 537,8 νм) и He-Sr (λ=430,5 νμ) лазерах при катафорезной прокачке паров. Причем, в He-Sr лазере были достигнуты рекордные для этого лазера значения удельной средней мощности (277 мВт/см3) и коэффициента усиления (0,15 см-1).В данной работе на примере активной среды He-Sr рекомбинационного лазера проведено теоретическое исследование процессов установления во времени продольного и радиального распределения паров металла в условиях импульсно-периодического разряда. Для этого были построены математические модели продольного и поперечного катафореза, применимые к импульсно-периодическим ионным ЛПМ.Для уравнения, описывающего распределение паров металла по длине разрядного канала, было получено следующее выражение:
где β = (θeE0L)/(kT)∙fτi, θ - степень ионизации, e - заряд электрона, T - температура газа, E0 - начальная напряженность электрического поля в импульсном разряде, L - расстояние от испарителя до катода, f - частота следования импульсов, τi - длительность импульса тока, D - коэффициент диффузии атомов стронция. При этом считается, что ионизирован, в основном, металл и что коэффициенты диффузии ионов гелия и стронция одного порядка. Решение уравнения (1) имеет вид:
где N(z,? ) есть решение стационарного уравнения диффузии [2]; для области испаритель-катод (0 ≤ z ≤ L) коэффициенты a k определяются по формуле:
Для функций, описывающих радиальное распределение концентраций ионов гелия, стронция и атомов стронция, была получена система из трех дифференциальных уравнений в частных производных. Для того, чтобы эта система стала применима к импульсно-периодическому режиму, входящие в нее параметры были усреднены по множеству импульсов. При усреднении полагалось, что тройная электрон-ионная рекомбинация имеет место только в послесвечении, а ионизация - в период протекания импульса тока. Скорости этих процессов вычислялись при характерной для соответствующего периода электронной температуре. В качестве характерной температуры электронов в течение импульса тока была взята температура 3 эВ, а в послесвечении - 0.1 эВ. Результирующая система уравнений, описывающая временную эволюцию радиальных предымпульсных (т.е. усредненных за большое число импульсов) концентраций частиц имеет вид:
здесь концентрации частиц нормированы на концентрацию атомов стронция у стенки трубки и введены безразмерные переменные x = r/R, τ = D/R2∙t, параметры a , b и g определяют скорость ионизации атомов He и Sr, а w - скорость тройной электрон-ионной рекомбинации. Система уравнений (3) решалась численно.На основании проведенных расчетов было установлено:
Литература [ 1] Латуш Е.Л., Чеботарев Г.Д., Васильченко А.В., Оптика атмосферы и океана, 11, 171-175 (1998).[2] Sosnowski T.P., J. Appl. Phys., 40, 5138-5144 (1969). |
| (c) АСФ России, 2001 |
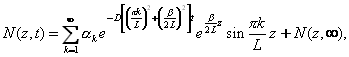 (2)
(2)