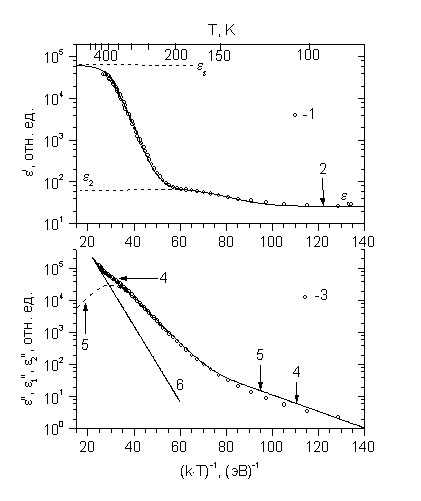
Научный руководитель: Суржиков Анатолий Петрович, доктор физ.-математических наук
Соавторы: Пешев Владимир Викторович

Удельная проводимость, комплексная диэлектрическая проницаемость , тангенс угла диэлектрических потерь существенно влияют на распространение электромагнитных волн в ферритах и, тем самым, определяют их функциональные возможности. Необходимо знать зависимости и от угловой частоты в широком диапазоне, примерно (10³-10¹⁰ ) rad/s, что важно для прогнозирования технических характеристик приборов на различных частотах.

Поэтому важно определять наиболее простым способом такие величины как статическую , и оптическую диэлектрические проницаемости, значения параметров релаксаторов, характеризующих их переориентацию, значения величин, характеризующих удельную проводимость и, используя эти величины, рассчитывать значения , , для интересующих частот при различных температурах.

Путем измерения емкости и полной активной проводимости мостовым методом были получены температурные зависимости действительной e ' и мнимой e '' частей диэлектрической проницаемости Li-Ti феррита двух видов: с энергией активации проводимости на постоянном токе U_ds =0.25 эВ ("низкоомные") (рис.1) и U_ds =0.54 эВ ("высокоомные" образцы) (не показана) [1].

Измерения проводились на частоте 1 МГц при напряжении измерительного сигнала 250 мВ в интервале температур (77-500 К). Обнаружены два типа диполей. Методом регрессионного анализа полученных зависимостей определены значения статических и оптических диэлектрических проницаемостей, значения энергий активации проводимости Us , характеризующих перенос носителей заряда в переменном электрическом поле. Также получены значения энергии переориентации диполей U₁, U₂ и значения предэкспоненциальных факторов t ₀₁ и t ₀₂. С использованием приведенных значений величин, была получена зависимость тангенса угла диэлектрических потерь tgd от температуры для низкоомных (рис. 2) и высокоомных образцов (не показана) [2, 3].

Для низкоомных образцов: ε_s,= (6.2+ 0.1)·10⁴; e ₂=70; t ₀₁=(1.6+ 0.5)·10^-9(с); U₁=(0.06+ 0.004) (эВ) t ₀₂=(1.38+ 0.06)Ч 10^-9 (с); U₂=(0.161+ 0.001) (эВ); s ₀=(47+ 3)·10¹³(Ом·см); Us =(0.272+ 0.002) (эВ); e _?=26.

Для высокоомных образцов: ε_s=50+ 1; e _?=18.7; t ₀₂=(2.0+ 0.3)·10^-9 (с); U₂=(0.159+ 0.005) (эВ); s ₀=(116+ 14) (Ом·см); Us =(0.583+ 0.005) (эВ). имеет смысл статической диэлектрической проницаемости при отсутствии диполей второго типа (рис.1).

Как в высокоомных, так и в низкоомных образцах энергии активации проводимости, измеренные в постоянном U_ds и переменном Us электрических полях приблизительно равны. Использование значений определенных параметров и w как аргумента дает возможность построения для заданной температуры прогнозируемых частотных зависимостей tgd (w ), e ' (w ), e '' (w ), в широком диапазоне частот. Однако критерием истинности прогнозируемых зависимостей должно являться их сопоставление с электрофизическими характеристиками ферритов, полученными экспериментально в рабочем диапазоне частот. Поэтому выполнение такого рода исследований является задачей следующего этапа нашей работы.