|
Продольные колебания системы с распределенными параметрами применительно к бурильным колонам Донецкий национальный университет Научный руководитель: Шевченко Феофан Леонтьевич, Доктор технических наук В настоящее время шахтные стволы разрабатываются буровыми установками роторного типа. Буровой инструмент (бур) с утяжелителем опускают в забой при помощи талевой установки на бурильных трубах. Бурильная колона испытывает кручение, растяжение-сжатие и изгиб. В работе рассматривается осевое напряженно деформируемое состояние от динамического воздействия нагрузок. В связи большими длинами трубных ставов в расчетной схеме бурильную колону следует рассматривать как систему с распределенными параметрами при наличии большой сосредоточенной массы на нижнем конце. Итак, получаем расчетную схему в виде однородного стержня длины l с погонной массой m и жесткостью EF, в верхнем сечении которого имеется упругая связь с коэффициентом жесткости с и сосредоточенной массой M на нижнем конце. Расчет бурильной колоны сводится к решению известного волнового уравнения
где u - продольное перемещение сечений, с - скорость волны деформации, q(x,t) - интенсивность возмущающей нагрузки. В работе описаны ударные процессы в двух вариантах загружения: при наращивании бурильной колоны и её спуске в скважину, а так же при подъеме оборванного бура, который при падении задержался в произвольном сечении ствола.В первой задаче рассматривается воздействие скорости движения става при внезапном защемлении его верхнего сечения. В этом случае жесткость с= ? . Уравнение (1) будет однородным, решение можно представить в виде
где U0 и N0 перемещение и усилие в начале координат, k - волновой вектор,w - частота, m - фаза. При выборе начала координат в верхнем сечении из граничных условий
получаем частотное уравнение
Начальные условия
где e(x)-единичная функция, учитывающая наличие скорости движения во всех сечениях, кроме защемленного. Из первого получим tan(m )=0, а из второго получим уравнение движения
позволяющие найти напряжение в любом сечении колоны. Из этого расчета получены предельные скорости движения колоны в зависимости от ее длины. Вторая задача с граничными условиями
получаем частотное уравнение
Из начальных условий (такие же как и первой задаче) получим уравнение движения сечений
На основании этой формулы решена задача о вычислении динамической нагрузки на бурильную колону при извлечении оборванного бура в момент срыва его с опоры. |
| (c) АСФ России, 2001 |
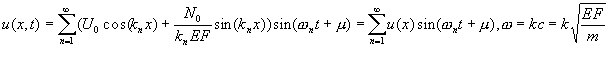 (2)
(2)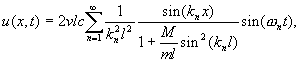 (6)
(6)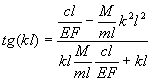 . (8)
. (8) (9)
(9)