|
Размерный эффект межфазной энергии на границе тонкая металлическая нить-диэлектрическая среда Кабардино Балкарский государственный университет Научный руководитель: Созаев Виктор Адыгеевич, д.ф.м.н. В последнее время в литературе стало уделяться большое внимание нанопроводам, как элементам электроники XXI века. Однако данные о межфазной энергии на границе тонкая металлическая нить – диэлектрическая среда встречаются крайне редко. В связи с этим в настоящей работе в рамках метода функционала электронной плотности рассматривается влияние диэлектрической среды на межфазную энергию тонких нитей. Рассмотрим задачу о вычислении поверхностной энергии бесконечно длиной тонкой нити радиусом R0. Воспользуемся цилиндрической системой координат.Плотность положительного заряда внутри нити зададим в виде ступенчатой функции n+(r):
где r - координата, перпендикулярная оси нити; n0 - плотность ионного заряда в массивном металле.Распределение электронной плотности на межфазной границе зададим в виде пробных функций:
где b -вариационный параметр, минимизирующий межфазную энергию s, RG – гиббсова координата раздела, которая находится из условия сохранения заряда нити:
где q s – поверхностная плотность заряда на межфазной границе нить - диэлектрическая среда.Распределение электростатического потенциала в нити находится
из уравнения Пуассона с учетом граничных условий
Из уравнения Пуассона (4) с учетом (1) и (2) получим выражения для распределения электростатического потенциала на межфазной границе нить - диэлектрическая среда: При RG<R0
При RG>R0
где
Вычисление поверхностной энергии проведем по формуле
где Минимизация межфазной энергии Вычисления проводились для нитей щелочных металлов радиусом порядка 10-30 а.е. Полученные нами результаты позволяют сделать следующие выводы:
|
| (c) АСФ России, 2001 |
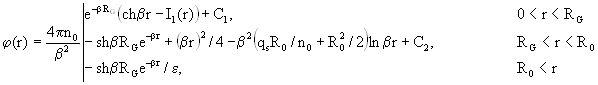 (5)
(5)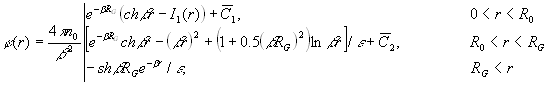 (6)
(6)