|
Критерии отбора олимпиадных задач по физике Рязанская государственная сельскохозяйственная академия Научный руководитель: Пащенко Василий Михайлович, Д.б.н., (Агрофизика) Опыт работы в сельской школ в качестве учителя физики заставляет задуматься над критериями отбора задач для школьных и районных физических олимпиад. Эта проблема стала актуальна сейчас как никогда ввиду расслоения системы образования на городскую и сельскую. Я имею ввиду, что селу с его невысоким научным потенциалом и средним общим образованием тяжело тягаться со специализированными школами с физико-математическим уклоном, где в качестве учителей физики работают преподаватели вузов и физика изучается на качественно другом уровне. Особенно это проявляется при столкновении интересов этих двух образовательных систем на предметных олимпиадах. Но прежде чем изложить суть проблемы более подробно хотелось бы напомнить, что из себя представляют олимпиады в настоящее время. Проведение физической олимпиады, как педагогического мероприятия преследует несколько целей: 1) популяризация физики, как науки и школьного предмета; 2) возможность каждому ученику проявить себя и свой талант (олимпиада должна носить массовый соревновательный характер); 3) выявить самых талантливых и способных учащихся.
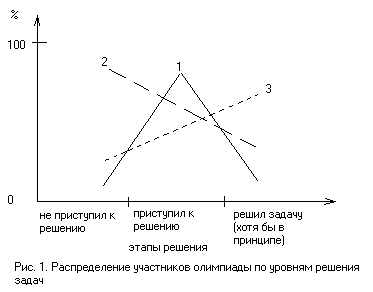
Графически это проиллюстрировано на рис 1, где по вертикальной оси отложена доля учащихся находящихся на данном этапе решения задачи (горизонтальная ось). Идеальный вариант олимпиадного задания выглядит следующим образом. Кривая 1 (задание средней сложности) симметричная относительно вертикальной оси характеризует то, что данное задание подобрано достаточно удачно и именно оно раскрывает массовый соревновательный характер олимпиады, то есть это задача, которая по силам учащимся со средними способностями. Кривая 2 (задание повышенной сложности), которая характеризуется падающим (слева направо) характером распределения участников по степени решения задачи решает проблему отбора победителя. Кривая же 3 (относительно простое задание) решает задачу развития у учащихся интереса к олимпиаде и физике в целом. Причем необходимо учитывать и возрастной фактор. Однако экспертиза олимпиадных заданий зачастую приводит совершенно к противоположной картине. Особенно это заметно в среде представителей сельских школ. Они зачастую бывают просто задавлены уровнем сложности олимпиадных заданий. Этот факт легко наблюдается при графической интерпретации результатов, где село расположилось на кривой 2, то есть большинство участников олимпиады не справилось с заданием. Причем эта черта все более и более отчетливее проявляется с ростом уровня олимпиады от школьной к районной, от районной к областной. Совершенно очевидно, что задания не учитывают специфику сельских школ. Поэтому необходимо разработать систему отбора задач для физических олимпиад, которая могла бы исключить указанные выше проблемы. Наиболее логичный и простой путь решения данной проблемы - замена одного задания в комплекте олимпиады для сельских школ. Это не повлияет существенно на картину результатов олимпиады в целом, но поднимет престиж сельских школ. Другой, более сложный путь - дифференцированный подход к участникам олимпиады, который может быть реализован через разбиение задания на два блока: "простых" и сложных задач. Решение задач отдельного блока оценивается соответственно суммой баллов Х 1 и Х2. Критерий отбора победителя - суммарный балл Х1+Х2. Но встает вопрос о отделении талантливых участников от массы участников, которые набрали большинство баллов за счет решения задач "простого" блока. Эта проблема легко разрешима при введении разности h =Х2-Х1. Сравнивая h с нулем можно легко вычислить в какой плоскости задач участник набрал большее количество баллов. Критерий h вступает в силу, если суммарный балл нескольких участников не позволяет выбрать победителя (например, баллы равны). Данная система должна позволить участвовать и бороться за победу всем учащимся на равных, не зависимо от географии их проживания.Другой не менее интересный вопрос - как отобрать задачи на олимпиаду. Для "простых" теоретических задач, решающих проблему популяризации физики и придания олимпиаде соревновательного характера в качестве данного параметра можно выбрать систему "число явлений - число уравнений", которая может характеризовать трудности, которые возникнут с решением задачи у учащихся. Вторая же часть выбранного критерия - число уравнений, характеризует математические сложности, которые могут возникать при решении задачи. Хотелось бы отметить, что данные критерии не равнозначны, т.е. количество явлений и уравнений не всегда равны между собой (пример: абсолютно неупругий удар). Согласно данной системы можно оценивать сложности, которые могут возникнуть при решении теоретических задач "простого" блока. Сложнее дело обстоит с оригинальными и экспериментальными задачами. Наиболее объективная оценка сложности этих задач должна быть поручена экспертам. В качестве экспертов можно выбрать учащихся школ, студентов. Причем задачи, рекомендованные для олимпиады в 9 классе необходимо давать на экспертизу в 10 и т.д., чтобы исключить возможность пересечения с данным заданием в непосредственно на олимпиаде. Количественно сложность задачи легко оценивается составлением статистического ансамбля по образцу на рис. 1. |
| (c) АСФ России, 2001 |