|
Нелинейные плазменные колебания в полупроводниковой сверхрешетке Волгоградский государственный педагогический университет Научный руководитель: Крючков Сергей Викторович, Доктор физико-математических наук В данной работе задача о колебаниях электронной плазмы в сверхрешетке (СР) сведена к решению интегро-дифференциального уравнения. С учетом периодичности электронного энергетического спектра по составляющей квазиимпульса вдоль оси СР уравнение, описывающее плазменные колебания, преобразовано в обыкновенное дифференциальное уравнение третьего порядка относительно безразмерного электрического поля плазменного колебания. Данное уравнение не имеет точного аналитического решения, и анализировалось с применением численных методов. Приведено сравнение найденного численного решения с приближенным решением, полученным методом Крылова - Боголюбова в условиях малой диссипации. Анализ проводился с помощью математического пакета Maple V, а также путем прямой реализации метода Рунге-Кутта для систем обыкновенных дифференциальных уравнений на языке программирования Turbo Pascal 7.0. В приближении слабостолкновительной плазмы, данная задача была решена аналитически. С учетом того, что спектр электрона в сверхрешетке описывается уравнением
и время действия излучения значительно превышает время релаксации электронов, т. е.
(пространственная зависимость векторного потенциала опускается, так как колебания полагаются однородными). Здесь
Такое преобразование возможно благодаря наличию периодической функции в подынтегральном выражении, обусловленной периодическим характером движения электрона в мини-зоне. В общем случае поле однородных плазменных колебаний в полупроводнике со сверхрешеткой описывается следующим из (3) нелинейным уравнением третьего порядка
Диссипация полагается малой, т. е. Здесь Ограничиваясь нулевым по
Его решение в терминах эллиптических функций Якоби:
Здесь
Под действием диссипации, величины Так, если Численный анализ уравнения (4) приводит к следующим результатам. 1) Экспоненциальный спад амплитуды справедлив лишь для
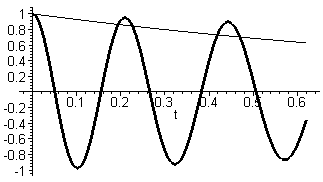
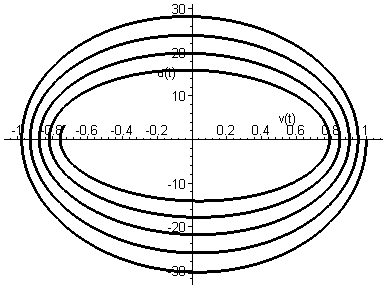
2) Частота плазменных колебаний с ростом времени убывает (как и следует из аналитического приближения). Однако анализ графиков численных решений (рис.1) позволяет оценить изменение частоты при любой диссипации. 3) Анализ был проведен для всех исследованных аналитически частных случаев. |
| (c) АСФ России, 2001 |
 (1)
(1)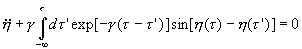 (2)
(2)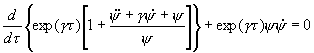 (3)
(3)