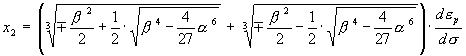Приложение теории катастроф к описанию упругопластической деформации материалов. Учет влияния внешних факторов.
Тихомирова Ирина Сергеевна
Ивановский государственный университет
Научный руководитель: Лев Николаевич Маурин, доктор физико-математических наук
Представленная работа является продолжением статьи "Приложение теории катастроф к описанию упругопластической деформации материалов. Ч. 1. Изотропное тело" [1] данного сборника. Еще раз повторимся, что мы рассматриваем упругопластическую деформацию с позиций теории катастроф.
Интерес к этой теме возник в связи с существованием многочисленных экспериментальных данных, указывающих на не "типичное" поведение материалов в процессе пластического деформирования. Здесь под словом не "типичное" мы подразумеваем появление скачков на диаграммах нагружения.
Известно, что на появление и форму скачков оказывают влияние различные факторы, как внешние (температура, скорость деформации, размер образца и т.д.), так и внутренние (примеси, границы зерен и т.д.). Существует ограниченная область температур Т и скоростей деформаций  , в которой наблюдаются скачки. Так, например, в [2] получено выражение, описывающее границы области существования скачкообразной деформации. Таким образом, скорость деформации и температура являются важными макроскопическими факторами, которые нельзя не учитывать при построении модели. , в которой наблюдаются скачки. Так, например, в [2] получено выражение, описывающее границы области существования скачкообразной деформации. Таким образом, скорость деформации и температура являются важными макроскопическими факторами, которые нельзя не учитывать при построении модели.
В работе [1] была рассмотрена простейшая модель, не учитывающая влияние Т и . Вследствие чего в области пластического деформирования было получено два устойчивых решения (возрастающее и убывающее). Но оба решения оказались равновероятными, и, поэтому, нельзя сказать определенно по какому пути будет развиваться деформация. Эти недостатки будут учтены в данной работе. . Вследствие чего в области пластического деформирования было получено два устойчивых решения (возрастающее и убывающее). Но оба решения оказались равновероятными, и, поэтому, нельзя сказать определенно по какому пути будет развиваться деформация. Эти недостатки будут учтены в данной работе.
Записывая функцию состояния упругопластического материала в виде
 , (1) , (1)
где 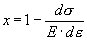 , мы подразумевали, что рассматриваем изотропный материал, то есть в этом случае переменная , мы подразумевали, что рассматриваем изотропный материал, то есть в этом случае переменная 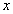 может входить в выражение Ф только в четных степенях. Однако теория катастроф утверждает, что какие бы физические факторы ни вступили в действие, выражение для Ф не может стать иным, кроме как может входить в выражение Ф только в четных степенях. Однако теория катастроф утверждает, что какие бы физические факторы ни вступили в действие, выражение для Ф не может стать иным, кроме как
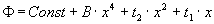 . (2) . (2)
Согласно сказанному выше, выражение для функции состояния упругопластического тела запишем в виде:
 . (3) . (3)
Здесь в зависимости от знака множителя перед 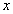 мы получаем две функции. В первом случае, когда скорость деформации мы получаем две функции. В первом случае, когда скорость деформации 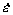 больше нижнего критического значения больше нижнего критического значения 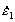 , но меньше верхнего критического значения , но меньше верхнего критического значения 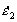 , и температура Т больше , и температура Т больше 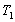 , но меньше , но меньше 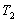 (то есть удовлетворяется условие существования скачкообразной деформации), функция состояния имеет вид (то есть удовлетворяется условие существования скачкообразной деформации), функция состояния имеет вид
 . (4) . (4)
Если хотя бы один из внешних факторов (или  , или , или 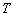 , или и , или и 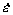 , и , и 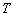 ) не принадлежат области существования скачкообразной деформации, тогда Ф, согласно (3), запишется так ) не принадлежат области существования скачкообразной деформации, тогда Ф, согласно (3), запишется так
 . (5) . (5)
Далее, в соответствии с методами теории катастроф, исследуем функции Ф на устойчивость. Экстремальными точками будут
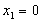 (6) (6)
и 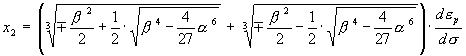 . (7)
Отметим здесь, что комплексные корни мы не учитываем. Легко проверить, что 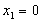 устойчиво области упругого деформирования и неустойчиво в пластической области. Что касается решения устойчиво области упругого деформирования и неустойчиво в пластической области. Что касается решения 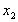 , то оно устойчиво в пластической и вырождается в , то оно устойчиво в пластической и вырождается в  в упругой области. в упругой области.
Тогда из (4) получаем 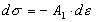 (убывающее решение), а из (5) следует, что (убывающее решение), а из (5) следует, что 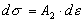 (возрастающее решение), где (возрастающее решение), где  ,  - не отрицательные функции - не отрицательные функции 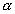 и и  , по модулю равные соответственно множителю в скобках перед , по модулю равные соответственно множителю в скобках перед 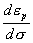 в равенстве (7). Здесь также как и в [1] в равенстве (7). Здесь также как и в [1] 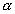 и и  в общем случае зависят от степени деформации, и должны определяться экспериментально. Таким образом, приращение напряжения не обязательно зависит от приращения полной деформации по линейному закону. Отметим также, что когда в общем случае зависят от степени деформации, и должны определяться экспериментально. Таким образом, приращение напряжения не обязательно зависит от приращения полной деформации по линейному закону. Отметим также, что когда 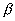 становится равным нулю, пластическая деформация прекращается, и тело будет (в соответствии с моделью) деформироваться упруго. Если же тело начинают разгружать на любой стадии деформации, то выполняется закон Гука (смотрите (3)). становится равным нулю, пластическая деформация прекращается, и тело будет (в соответствии с моделью) деформироваться упруго. Если же тело начинают разгружать на любой стадии деформации, то выполняется закон Гука (смотрите (3)).
Выводы:
- в работе представлена макроскопическая модель упругопластического тела, которая описывает деформационную зависимость, характерную для эффекта Портевина - Ле Шателье.
Список литературы:
Тихомирова И.С. // Настоящее издание. С.
Г.А. Малыгин. ФММ 63, 5, 864 (1987).
|
 , (1)
, (1) . (3)
. (3) . (4)
. (4) . (5)
. (5)