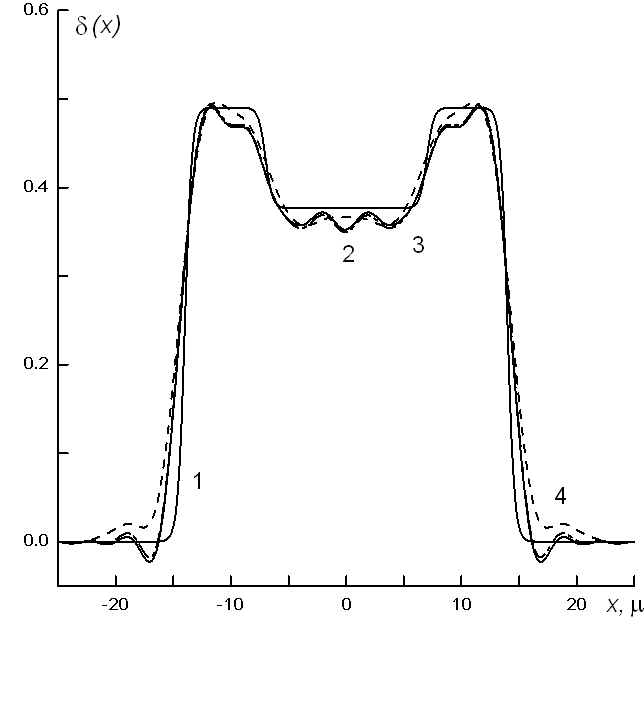
Научный руководитель: Бушуев Владимир Алексеевич, доктор физмат наук

Метод фазового контраста позволяет повысить контраст изображения в десятки раз по сравнению с обычно используемыми абсорбционными методами. Особенно это важно для изучения внутренней структуры медико-биологических объектов, в которых коэффициент поглощения m(x, z) мал в силу их небольшой плотности. Кроме этого, метод очень эффективен для исследования слабопоглащающих объектов с слабыми вариациями коэффициента поглощения внутри объекта - для метода важны вариации коэффициента преломления d(x, z) в исследуемом объекте [1,2].

В настоящем докладе представлено решение обратной задачи метода рентгеновского фазового контраста для методики получения фазоконтрастных изображений без использования кристалла-анализатора [2]. В качестве исследуемого объекта моделировался капилляр из полиметилметакрилата (ПММА), заполненый этиловым спиртом. Радиус внешних стенок капилляра r₁ = 14 m m, радиус внутренних стенок r₂ = 7 m m, толщина переходного слоя D r = 0.3 m m. Коэффициенты поглощения стенок капилляра и жидкости в канале соответственно m ₁ = 0.493 cm^-1 и m ₂ = 0.369 cm^-1 а декременты преломления соответственно d ₁ = 0.49× 10^-6 и d ₂ = 0.377× 10^-6 для длины волны источника ренгеновского излучения AgKa l = 0.05594 nm. Данный объект моделирует кровеносный сосуд (рис.1, кривая 1), и его физические характеристики близки к истинным. Величина статистического шума интенсивности фазоконтрастного изображения капилляра (рис.1, кривая 2) была положена 7% (рис. 1, кривая 3). Размеры активного зерна фотопластинки были взяты в пределах от 1 до 4 m m.

1. Для данной методики получения фазоконтрастных изображений решение обратной задачи по восстановлению декремента преломления из искаженных данных интенсивности с погрешностью, не большей погрешности интенсивности, возможно лишь для фотопластинки с размером активного зерна не более 1 m m.
2. В силу особенностей данной методики восстановление декремента преломления объекта, размерами большими 50 m m, с погрешностью не большей погрешности интенсивности, для фотопластинки с размерами активного зерна большими 5 m m, невозможно.

Рис. 1. Фазоконтрастные изображения для капилляра ПММА-этиловый спирт для методики без использования кристалла-анализатора. Внешний радиус капилляра 14 m m. Статистический шум D I = 7%. Размеры зерна фотопластинки 1 m m. Кривые 1 - поперечный профиль декремента преломления d капилляра в единицах 10^-6, 2 - точное значение фазоконтрастной интенсивности капилляра в случае отсутствия статистических шумов, 3 - в случае наличия шумов.

Рис. 2. Решения обратной задачи восстановления декремента преломления d . Кривые 1 - теоретическая модель декремента преломления капилляра, 2 - результат восстановления декремента из кривых интенсивности 2 рис. 1, 3 - результат восстановления кривых 3 рис. 1, 4 - результат восстановления из сглаженных фотопластинкой данных кривых 3 рис. 1.