|
Исследование фазового равновесия кристалл - жидкость методом молекулярной динамики Воронежский государственный технический университет Научный руководитель: Хухрянский Юрий Павлович, доктор физико-математических наук Разработана микроскопическая модель фазового равновесия в системе раствор-расплав Ga-P - твердая фаза GaP. Проведен численный анализ модели на ЭВМ с использованием метода молекулярной динамики. В основе модели жидкая система из 4000 атомов галлия и 500 атомов фосфора, помещенных в куб с размером ребра L. Взаимодействие между частицами описывается потенциалом Леннарда-Джонса:
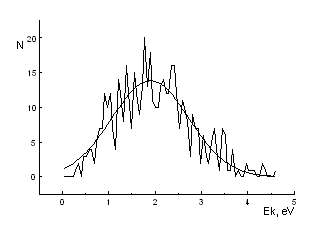
где R — расстояние между частицами, а D, R0, n и m - параметры потенциала.В плоскости ху на систему налагаются условия периодичности с периодом L. Верхняя стенка куба является отражающей. Нижняя граница представляет собой пленку полупроводникового соединения А3В5 - фосфида галлия. Это соединение имеет решетку типа цинковой обманки, которую можно представить как две вставленные друг в друга гранецентрированные кубические решетки. В качестве активного слоя подложки предполагалось брать одну элементарную ячейку с периодом “а”, транслируемую по всей нижней поверхности молекулярно-динамической ячейки.Температура в системе задавалась постоянной - 1270 К. Она моделировалась исходя из величины скорости частиц в системе и нормировки этой величины на каждом шаге. При этом периодически вычислялось распределение Максвелла по скоростям, чтобы судить о поведении системы (см. рис. 1) .Основная трудность молекулярно-динамического моделирования связана, как известно, с тем, что для расчета сил, действующих на частицы, необходимо на каждом шаге по времени вычислять все расстояния между частицами. Число таких расстояний равно N(N - 1)/2, поэтому объем вычислений растет пропорционально N 2. Наиболее точный способ избежать квадратичного роста времени счета, с увеличением числа частиц, был предложен Верле. Он состоит в определении матрицы ближайших соседей, которые только и учитываются при вычислении межчастичных расстояний. С этой целью вводятся радиус обрезания взаимодействия rc и радиус горизонта rg. Частицы, находящиеся от данной на расстоянии, не превышающем rg, считаются ее ближайшими соседями. Во взаимодействии участвуют только частицы из сферы взаимодействия rij < rc Частицы, расположенные между сферами с радиусами rc и rg, образуют буфер, между которым и сферой взаимодействия происходит обмен частицами. Матрица соседей обновляется через каждые 30 шагов по времени.Основным графиком, полученным на основе моделирования, является зависимость количества десорбируемых атомов фосфора с поверхности кристаллического фосфида галлия от времени при различных значениях величины потенциального барьера Е 2 на границе кристалл – жидкость (см. рис. 2).
Из графика можно проследить экспоненциальный характер зависимости N от E 2. Величиной барьера Е2 мы варьировали исходя из параметров потенциала Леннарда – Джонса, описывающего взаимодействие между адатомами фосфора на поверхности пленки и атомами, составляющими эту пленку. Также учитывалось взаимодействия между адатомами фосфора. Это взаимодействие определяло характер поведения атомов фосфора на поверхности кристаллического фосфида галлия. С повышением концентрации адатомов фосфора на моделируемой подложке происходило увеличение потока атомов фосфора с поверхности пленки. В дальнейшем это приводило к восстановлению равновесия потоков атомов фосфора, т.к. концентрация атомов фосфора в расплаве галлия и температура расплава поддерживались постоянными.Таким образом, расчет показал возможность применения метода молекулярной динамики для моделирования процессов, происходящих на межфазной границе раствор-расплав – твердая фаза. Были получены качественные и количественные характеристики, хорошо описывающие фазовое равновесие в первом приближении. В последующем компьютерная модель будет предполагать возможность образования димера Р 2 на поверхности подложки, его диффузию и возможность распада в расплаве. |
| (c) АСФ России, 2001 |
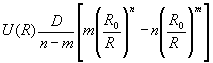 , (1)
, (1)