|
Точность определения параметров в различных приближениях теории интенсивностей Витебский государственный университет Научный руководитель: Корниенко Алексей Александрович, доктор физ.-мат. наук Точность определения параметров в различных приближениях теории интенсивностей исследуется на примере стекол, активированных ионами празеодима. Интерес к синтезу и исследованию спектральных свойств стекол различного состава, активированных ионами празеодима, объясняется тем, что при низкой трудоемкости изготовления лазерных стекол, они имеют оптические качества и механическую прочность близкую к кристаллам. Стекла, активированные трехвалентным празеодимом, обладают очень богатым спектром излучения, простирающимся от ультрафиолетовой области до инфракрасной. Такие стекла одни из наиболее перспективных кандидатов для создания лазеров, работающих на длине волны 1.3 мкм и необходимых для оптоволоконных линий связи. О выполнении достаточных условий генерации судят не только по структуре энергетических уровней, но и по времени жизни уровней и по коэффициентам ветвления люминесценции с них. Силы линий межмультиплетных электрических дипольных переходов оценивают в одном из приближений конфигурационного взаимодействия: слабого
промежуточного
или сильного
Здесь Зная силы линий, можно легко вычислить силы осцилляторов переходов
где После этого нетрудно вычислить другие важные характеристики : время жизни возбужденного уровня
и коэффициенты ветвления люминесценции с этого уровня
где
Определение адекватного приближения для описания спектральных свойств лазерных стекол непростая проблема. В данной работе предлагается в качестве дополнительного критерия адекватности использовать информацию о погрешности параметров интенсивности. Погрешности параметров определены для стекол различного состава. Было установлено, что в приближении слабого конфигурационного взаимодействия погрешности параметров интенсивности получаются самыми большими и значение параметра Для определения погрешностей использовался алгоритм, разработанный автором и удобный с точки зрения компьютерного применения. Суть предлагаемого алгоритма сводится к следующему: а) минимизируя компьютерными методами сумму квадратов отклонения теоретических значений физических величин от экспериментальных, в первую очередь, определяются оптимальные значения параметров и среднеквадратичное отклонение б) используя оптимальные параметры, на основе матричных или аналитических уравнений вычисляются оптимальные значения физических величин; в) в дальнейших вычислениях все параметры кроме одного, для которого вычисляется погрешность, фиксируются. Выбранный параметр варьируется до тех пор пока среднеквадратичное отклонение вычисленных физических величин от оптимальных не станет равным Полученное отклонение выделенного параметра от его первоначального оптимального значения и есть погрешность. |
| (c) АСФ России, 2001 |
 (2)
(2) (3)
(3)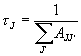 (4)
(4)