|
Моделирование двухфазной гетерогенной системы жидкость-газ методом молекулярной динамики Воронежский государственный технический университет Научный руководитель: Хухрянский Юрий Павлович, доктор физ.-мат. наук Объектомрассмотрения данной работыявлялась двухфазная система жидкость-газ, длямоделирования которойприменялся метод молекулярной динамики. Предполагалось, что в начальныймомент времени в конденсированной фазе находятсятолько молекулы нелетучегокомпонента (растворителя), а в газовой тольколетучего. Нелетучий компонентсуществует в виде одноатомных молекул,летучий компонент существует вгазовой фазе только в виде димеров, а вконденсированной фазе -как в виде одноатомных молекул, так и в видедимеров. Ассоциация идиссоциация двухатомных молекул летучегокомпонента происходит в жидкойфазе. Такое состояние соответствует растворамтипа АIII-BV.Вкачестве потенциаламежмолекулярного взаимодействия был выбранпотенциал Леннарда-Джонса ( 12-6):
где rij -расстояние между iи j молекулами, e-характеристическая энергия,s - равновесное межмолекулярноерасстояние.При моделированиинегомогенных систем время установления равновесия(появление квазистационарногомежфазного потока) значительно больше, чемдля гомогенных систем. В связи сэтим в данной работе мы ввели следующееприближение: на каждом шагеопределялись координаты и скорости толькомолекул летучего компонента.Естественно, что для определения траекторийдвижения этих молекулнеобходимо учитывать воздействие молекулнелетучего компонента, которыев основном и будут составлять ближайшееокружение каждой легкоймолекулы. Для этого на каждом шагеинтегрирования вокруг каждоймолекулы летучего компонента задавалась сфера радиусом2s. Внутри этой сферыслучайным образом задавались координатымолекул нелетучего вещества,число которых определялось размеромсферы и величиноймакроскопической плотности рассматриваемогораствора-расплава.Дальнейшие вычислениясил, скоростей и координатпроводились с учетом заданного ближайшегоокружения, а также другихмолекул летучего компонента . Описанное вышеприближение соответствуетситуации, когда на каждом шаге интегрированияближайшее окружение каждоймолекулы летучего компонента полностьюменяется. В связи с этим шагинтегрирования равнялся среднему временисвободного пробега молекуллетучего компонента в жидкой фазе:
где MB - масса молекулылетучего компонента, k - константа Больцмана,T - макроскопическаятемпература.Предполагалось, что ассоциациядимеров летучего компонента происходитпри столкновении двуходноатомных молекул. При этом, для образованиедимера, значение максимальнойпотенциальной энергии при столкновениидолжно превышать некотороекритическое значение Eас (энергияассоциации ). С учетом (1) и после преобразования, получаем условиеобразования димера пристолкновении двух одноатомных молекул:
Как и вслучае ассоциации, диссоциациядимеров летучего компонента происходиттакже при столкновении димера смолекулой. Условие диссоциации димерааналогично условию ассоциации( 3):
Нами был проведен ряд машинныхэкспериментов для системы содержащей впервоначальный момент 10 6молекул Ga, располагающихся вмолекулярно-динамическойячейке соответствующей объему жидкой фазы и 104 молекулP2, располагающихся вмолекулярно-динамической ячейкесоответствующей газовой фазе.
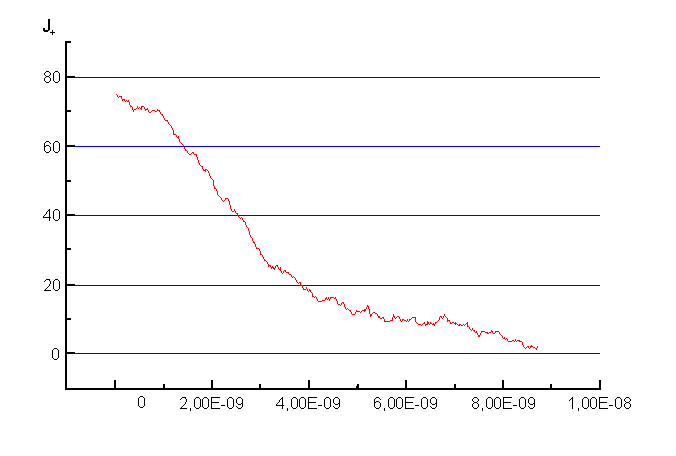
рис. 1Впервоначальный моментмолекулы находились в узлах простой кубической решетки.Размерымолекулярно-динамическойячейки вдоль поверхности раздела фазсоставляли L x=Ly=10-8 м. В направлении, нормальном кмежфазной поверхности, размерячейки выбирался исходя из значениймакроскопической плотностисоответственно для жидкой и газовой фазы. Шагинтегрирования составлял 10-13с, температура моделирования 1000К. Зависимость суммарного потокачерез межфазную поверхность приведена нарис 1. Полученная зависимостьхорошо согласуются с данными, полученнымиранее экспериментально и припомощи методов макроскопическогомоделирования. |
| (c) АСФ России, 2001 |
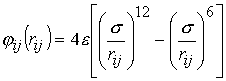 , (1)
, (1)