|
Частные решения задачи декомпозиции Дальневосточный государственный университет Научный руководитель: Кулешов Евгений Львович, Доктор технических наук Современные методы оценивания спектральной плотности стационарных случайных процессов можно условно отнести к двум типам: непараметрические (линейные) и параметрические. Во многих случаях непараметрические методы имеют недостаточную разрешающую способность, что особенно сказывается при анализе процессов с линейчатым спектром. Применение параметрических методов предполагает знание априорной информации, достаточной для построения параметрической модели исследуемого процесса. Если такая информация отсутствует, то применение параметрических методов может быть связано со значительными ошибками, возникающими из-за неадекватного выбора модели.Для вычисления непараметрических спектральных оценок высокого разрешения в работе [1] предлагалось использовать соотношение:
известное как спектральное представление стационарного случайного процесса
каждого слагаемого. В (2) интервал наблюдения
где
Для каждого
где В данной работе были получены два частных решения системы (3). Первое решение получено при условии
Получить аналитическое решение системы уравнений (3) в общем виде по нашему мнению невозможно, поэтому был рассмотрен случай, когда спектр сигнала
Решение системы (3) было получено методом Крамера (определителей) и имеет вид:
Проверка этого решения показала, что формулы (10), (11) определяют истинные значения амплитуд и фаз двух гармоник независимо от длины реализации На основе решения (10), (11) разработан алгоритм выделения гармонического сигнала на фоне гармонической помехи [1]. Список публикаций: [1 ] Е.Л. Кулешов, Декомпозиция стационарных случайных процессов на гармонические компоненты, как основа спектрального анализа высокого разрешения, Автометрия, 2000, №4, с. 26-35.[2] Е.Л. Кулешов, П.С. Чуднов, Частное решение задачи декомпозиции сигнала на гармонические компоненты, Препринт. Владивосток: ИАПУ ДВО РАН, 2000. 24 с. |
| (c) АСФ России, 2001 |
 (3)
(3)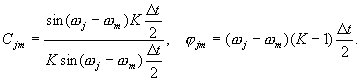 (6)
(6)