Фуллерено-подобные структуры как проекции многомерных регулярных решёток
Сабуть Андрей Вацлавович
Гродненский государственный университет
Научный руководитель: Лиопо Валерий Александрович, доктор физ.-мат. наук, профессор
Открытые в последнее время вещества (квазикристаллы, фуллерены, нанотрубки и др.) обладают симметрией, которая не может быть описана кристаллографическими группами трёхмерного евклидова пространства [1]. Поэтому, приобрели актуальность исследования регулярных решёток в пространствах с размерностями больше трёх, и последующие отображения этих решёток в трёхмерное пространство.
Пусть 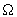 - регулярная решётка над кольцом целых чисел - регулярная решётка над кольцом целых чисел Z в n-мерном евклидовом пространстве 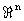 , заданная с помощью матрицы Грама G. Группа точечной симметрии решётки , заданная с помощью матрицы Грама G. Группа точечной симметрии решётки 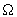 изоморфна мультипликативной группе изоморфна мультипликативной группе 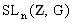 целочисленных матриц N, удовлетворяющих соотношению целочисленных матриц N, удовлетворяющих соотношению
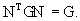 (1) (1)
Структура каждого элемента симметрии (ЭС) решётки 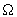 полностью определяется собственными значениями соответствующей матрицы полностью определяется собственными значениями соответствующей матрицы  , характеристический многочлен которой имеет вид , характеристический многочлен которой имеет вид
 (2) (2)
где  - многочлены деления круга [2]; - многочлены деления круга [2]; 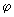 - функция Эйлера. Порядок такого ЭС равен m - наименьшему общему кратному чисел - функция Эйлера. Порядок такого ЭС равен m - наименьшему общему кратному чисел 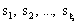 . Наименьшая размерность . Наименьшая размерность 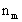 евклидова пространства, в котором существуют ЭС m-го порядка, определяется по формуле евклидова пространства, в котором существуют ЭС m-го порядка, определяется по формуле
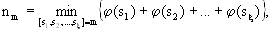 (3) (3)
где перебор проводится по всем совокупностям различных натуральных чисел  , 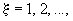 наименьшее общее кратное которых равно m. Матрицу Грама регулярной решётки, имеющей ЭС с характеристическим многочленом (2), можно определить как наименьшее общее кратное которых равно m. Матрицу Грама регулярной решётки, имеющей ЭС с характеристическим многочленом (2), можно определить как
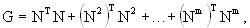 (4) (4)
где 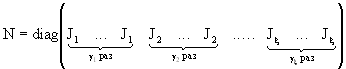 - квазидиагональная матрица, клетки - квазидиагональная матрица, клетки 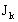 которой являются сопровождающими матрицами [3] для множителей которой являются сопровождающими матрицами [3] для множителей  , входящих в формулу (2), , входящих в формулу (2), 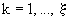 . Тогда . Тогда 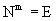 - единичная, и - единичная, и 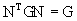 . Следовательно, . Следовательно,  и соответствует ЭС m-го порядка регулярной решётки с матрицей Грама (4). Например, решётки с ЭС 5-го, 8-го, 10-го, 12-го порядков не существуют в трёх-, но существуют четырёхмерном евклидовом пространстве. и соответствует ЭС m-го порядка регулярной решётки с матрицей Грама (4). Например, решётки с ЭС 5-го, 8-го, 10-го, 12-го порядков не существуют в трёх-, но существуют четырёхмерном евклидовом пространстве.
Определим ортогональную проекцию n-мерной регулярной решётки  на (n-k)-мерное подпространство вдоль k-мерной кристаллографической плоскости, порождённой k линейно независимыми векторами решётки на (n-k)-мерное подпространство вдоль k-мерной кристаллографической плоскости, порождённой k линейно независимыми векторами решётки  :
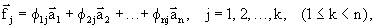 (5) (5)
где  - базис решётки. В пространстве - базис решётки. В пространстве 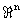 введём декартову систему координат введём декартову систему координат 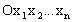 так, чтобы плоскостью проецирования совпадала с координатной плоскостью так, чтобы плоскостью проецирования совпадала с координатной плоскостью 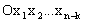 . Матрицу базисных векторов решётки . Матрицу базисных векторов решётки 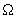 в системе в системе 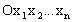 запишем в виде запишем в виде 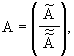 где где  - 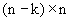 -матрица. Поскольку A - невырожденная, то среди столбцов матрицы -матрица. Поскольку A - невырожденная, то среди столбцов матрицы  должны найтись n-k линейно независимых. Составим из них квадратную матрицу должны найтись n-k линейно независимых. Составим из них квадратную матрицу 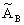 , а из остальных столбцов - матрицу , а из остальных столбцов - матрицу  , т.е. формально можно записать: , т.е. формально можно записать:
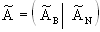 . (6) . (6)
Выразим  через через 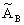 , т.е. , т.е. 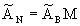 . Векторы (5) будут проецироваться в начало координат, значит . Векторы (5) будут проецироваться в начало координат, значит 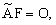 где где  , O - нулевая матрица. Это условие запишем несколько в развёрнутом виде , O - нулевая матрица. Это условие запишем несколько в развёрнутом виде 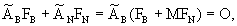 где матрица где матрица 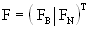 разделена в соответствии с (6). Откуда находим, что разделена в соответствии с (6). Откуда находим, что 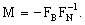 Так как матрица F состоит из целых чисел, то элементы матрицы M будут рациональными. Обозначим наименьший общий знаменатель элементов i-ой строки матрицы M через Так как матрица F состоит из целых чисел, то элементы матрицы M будут рациональными. Обозначим наименьший общий знаменатель элементов i-ой строки матрицы M через 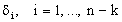 . Тогда декартовы координаты проекций векторов решётки . Тогда декартовы координаты проекций векторов решётки 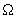 могут быть определены по формуле могут быть определены по формуле 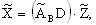 где где 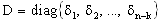 , 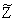 - матрица-столбец, состоящая из произвольных целых чисел. Следовательно, ортогональная проекция n-мерной регулярной решётки вдоль любой её k-мерной плоскости - матрица-столбец, состоящая из произвольных целых чисел. Следовательно, ортогональная проекция n-мерной регулярной решётки вдоль любой её k-мерной плоскости  представляет собой (n-k)-мерную регулярную решётку, матрица Грама которой представляет собой (n-k)-мерную регулярную решётку, матрица Грама которой
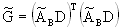 . (7) . (7)
Рассмотренная теория применена для построения ортогональных проекций многомерных решёток, имеющих ЭС 5-го, 8-го, 10-го и 12-го и др. порядков [4]. Эти проекции являются регулярными решётками, матрицы Грама которых определятся по формуле (7). Был выполнен анализ около 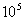 координационных полиэдров полученных проекций. Установлено, что некоторые из этих полиэдров имеют элементы симметрии граней порядков 5, 8, 9 и др. В связи с чем они были названы нами фуллерено-подобными структурами. Полученные полиэдры могут быть использованы в структурной физике твёрдого тела [5]. координационных полиэдров полученных проекций. Установлено, что некоторые из этих полиэдров имеют элементы симметрии граней порядков 5, 8, 9 и др. В связи с чем они были названы нами фуллерено-подобными структурами. Полученные полиэдры могут быть использованы в структурной физике твёрдого тела [5].
Список публикаций:
[1] Ле Ты Куок Тханг, Пиунихин С.А., Садов В.А., УМН., 48, № 1, 41-102 (1993).
[2] Ван дер Варден Б.Л. Алгебра. М.: Наука (1979).
[3] Гантмахер Ф.Р. Теория матриц. М.: Наука (1988).
[4] Сабуть А.В. Вестник ГрГУ, № 2, 23-39 (2000).
[5] Abe Eiji and Tsai An Pang., Phys. Rev. Lett., 83, № 4, 753-756 (1999).
|
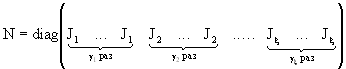 - квазидиагональная матрица, клетки
- квазидиагональная матрица, клетки 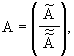 где
где