|
Топология мира Минковского Московский педагогический государственный университет Научный руководитель: Розгачёва Ирина Кирилловна, К. Ф.-М. Н. 1. Множество М{S} Минковский назвал четырёхмерным миром. В настоящей работе показано, что мир M{S} может иметь однородное и изотропное пространство-время, но с топологией четырёхмерного тора. Обозначим этот мир T{S}.2. В мире T{S} нет проблемы сингулярности. Линии времени мира T{S} могут оказаться замкнутыми, и тогда появляется так называемая проблема причинности, т. е. возможность возврата физической системы в собственное прошлое. В работе показано, что этой проблемы можно избежать.3. Мир T{S}. Для наглядности рассмотрим выражение
в двумерном случае: Переменная S может изменяться отОбозначим этот мир как Он имеет координаты:
Этот мир соответствует ускоренному движению частицы со скоростью Мир T{S} компактен.Рассмотрим события Введём евклидово пространство с тремя взаимно ортогональными координатами:
Дифференциал расстояния между близкими точками этого пространства равен:
Формула (1) определяет расстояние между точками на поверхности тора. События S(u, v) образуют поверхность тора с координатными линиями "u", "v". Координатная линия "v" есть меридиан тора, а координатная линия "u" есть параллель тора.Рассмотрим событие, для которого Введём евклидово пространство с тремя взаимно ортогональными координатами:
Координаты Координатные линии x и t замкнуты, т.к. бесконечному множеству значений x и t соответствует конечное множество событий S.Следует особо подчеркнуть, что физически допустимая траектория частицы в мире T{S} незамкнута.При перемещении от события |
| (c) АСФ России, 2001 |
 ;
;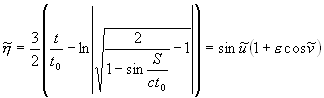 ;
;