|
Сверхпроводящая щелевая линия Ростовский государственный университет Научный руководитель: Лерер Александр Михайдович, доктор физико-математических наук Решена задача о распространении гибридной волны в сверхпроводящих щелевых и копланарных волноводах (рис.1).
Рис.1.Щелевая линия (а) и копланарный волновод (б). Влияние конечной проводимости сверхпроводников учтено с помощью приближенных граничных условий, имеющих вид (1), (2), (3):
где
где
Парные сумматорные уравнения (ПСУ), к которым сводится данная задача, решены методом Галеркина с базисом, учитывающим особенность поведение электромагнитного поля на ребре, благодаря которому решение бесконечномерной задачи сводится к решению системы линейных алгебраических уравнений(СЛАУ) небольшого порядка. При решении ПСУ проведена регуляризация задачи путем выделения особенности ядра ПСУ, проявляющейся в крайне медленной сходимости рядов, через которые выражаются матричные элементы СЛАУ. Для выделения особенности были найдены асимптотические выражения матричных элементов СЛАУ. Далее ряды разбивались на два, как показано в формуле (4):
Первый ряд легко считается численно. Второй считается аналитически. В соответствии с методикой решения задачи на языке C++ разработана программа для персональных компьютеров, позволяющая рассчитывать дисперсионные характеристики и потери в проводниках для четырехслойного щелевого или копланарного волновода. Проведенные исследования сходимости решения показали, что для расчетов с погрешностью не более 0.1% достаточно решать СЛАУ порядка 3-6. |
| (c) АСФ России, 2001 |
 ,
,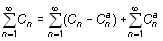 . (4)
. (4)