|
Метод исследования бассейнов притяжения аттракторов генератора "Torus" Саратовский государственный университет Научный руководитель: Короновский Алексей Александрович, к.ф.-м.н. Целью данной работы является исследование бассейнов притяжения аттракторов генератора "Торус" для различных фиксированных значений управляющих параметров. Генератор, предложенный Л. Чуа с соавторами в [1] представляет собой радиотехническую схему третьего порядка, содержащую нелинейный элемент, который имеет кусочно-линейную вольт-амперную характеристику. Схема описывается системой трех дифференциальных уравнений, полученных на основе законов Кирхгофа. Эта система может быть приведена к безразмерному виду:
где В работе [2] были построены многолистные двухпараметрические карты динамических режимов на плоскости управляющих параметров. В ходе работы безразмерная система (1) численно интегрировалась методом Рунге-Кутта четвертого порядка, строились фазовые портреты и сечения Пуанкаре для различных начальных условий при фиксированных значениях управляющих параметров при выбранном переходном процессе. Для данной системы характерна неоднозначность поведения (мультистабильность) на плоскости управляющих параметров. В точке с фиксированными параметрами a и g система может демонстрировать не один, а несколько режимов колебаний, в зависимости от начальных условий. Так как система обладает двумя собственными частотами, то наблюдаемые режимы удобно классифицировать исходя из чисел вращения [1].Для построения бассейнов притяжения аттракторов использовался следующий метод: на плоскости сечения Пуанкаре выбиралась точка начальных условий, для которой рассчитывалась фазовая траектория (при этом не отбрасывался переходный процесс) и определялся режим колебаний, когда изображающая точка выходила на аттрактор. Исходной точке начальных условий присваивался цвет, соответствующий данному режиму, кроме того, этим же цветом окрашивались точки сечения Пуанкаре, которые соответствовали установившемуся режиму, а также точки, попавшие в сечение при переходном процессе. Данный метод позволил существенно сократить время, необходимое для исследования. Этот метод позволяет также определить длительность переходного процесса для каждой точки начальных условий при фиксированных значениях управляющих параметров. Список публикаций: [1] Matsumoto T., Chua L.O., Tokunaga R.// IEEE Trans. Circuits and Syst. 1987. Vol.34 N 3. P.240. [2] Андрушкевич А.В., Кипчатов А.А., Красичков Л.В., Короновский А.А. Экспериментальное двухпараметрическое исследование неоднозначных режимов колебаний // Изв. вузов. Радиофизика. 1995. Т.38. N 11.С.1195. [3] Кипчатов А.А., Короновский А.А. Тонкие эффекты самоподобного поведения кусочно-линейной системы вблизи линии бифуркации рождения тора // Изв. вузов "ПНД", Т.5.N 2,3. 1997. |
| (c) АСФ России, 2001 |
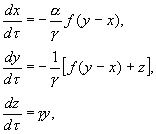 (1)
(1)