ВНКСФ7: Земляков Вячеслав Викторович: Электродинамический анализ электромагнитных полей в четырехгребневом прямоугольном волноводе

Электродинамический анализ электромагнитных полей в четырехгребневом прямоугольном волноводе

Земляков Вячеслав Викторович
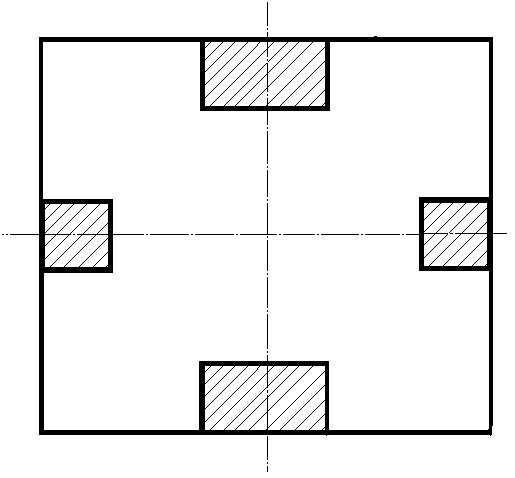
Ростовский государственный университет

Научный руководитель: Заргано Геннадий Филиппович, Доктор физико-математических наук

Волноводы со сложной формой поперечного сечения, к которым относится 4-х гребневый прямоугольный волновод, находят все более разнообразное применение при конструировании различных СВЧ устройств. Так квадратный четырехгребневый, как частный случай рассмотренного в данной работе прямоугольного волновода с четырьмя металлическими выступами, широко используют в качестве излучающих элементов антенных решеток (АР). Его функциональной особенностью является наличие двух вырожденных волн с ортогональной поляризацией. Такой двухполяризационный волновод представляет значительный практический интерес. В частности он позволяют образовывать периодические структуры сотового типа и улучшить характеристики линзовых антенн и АР.

В качестве метода расчета критических волновых чисел и компонент полей в 4-х гребневом прямоугольном волноводе с воздушным заполнением без потерь применялся метод частичных областей (МЧО) с учетом особенности электромагнитного поля на ребре. Он позволяет при минимальном времени счета получить максимально точные, по сравнению с другими методами, результаты расчетов, а также записать выражения для электромагнитных полей в аналитическом виде.

Учитывая свойства электромагнитных полей Н- и Е-волн относительно плоскостей симметрии четырехгребневого прямоугольного волновода, поперечное сечение разбивалось на четыре части и рассматривалась одна из них с изменяющимися граничными условиями на части внешнего контура (см. рис. 1).

рис. 1

Согласно МЧО площадь поперечного сечения полученной сложной области разбивалась на три простые частичные области. Записывалось решение двумерного уравнения Гельмгольца в каждой области для магнитных и электрических векторов Герца при различных граничных условиях в виде бесконечных рядов с неопределенными коэффициентами по собственным функциям частичных областей.

Собственные функции частичных областей записывались в соответствии с граничными условиями, а неизвестные коэффициенты разложения полей определялись через значения неизвестных функций - для Н-волн и - для Е-волн, заданных на линиях раздела частичных областей.

Из условия непрерывности H_z компоненты поля для Н-волн и H_y - для Е-волн на смежных границах частичных областей, получили системы интегральных уравнений Фредгольма 1-го рода относительно неизвестных функций с ядрами, имеющими логарифмическую особенность.

Системы интегральных уравнений решались с использованием приближенного метода Галеркина, в результате чего были получены линейные однородные системы уравнений. Приравняв определители систем к нулю, получили трансцендентные уравнения для определения собственных чисел для Н- и Е-волн. Опустив одно из уравнений каждой системы и сделав необходимые преобразования, пришли к линейным неоднородным системам уравнений, решение которых дало значения неизвестных коэффициентов с точностью до постоянного множителя, определяемого из условия нормировки.

Для построения картины распределения поля по поперечному сечению волновода использовали уравнения и . Первое уравнение описывает в поперечном сечении волновода структуру силовых линий электрического поля для Н-волн, второе - магнитного поля для Е-волн.

Разработанный алгоритм анализа реализован на языке программирования Borland C ++. В процессе расчетов на ЭВМ наблюдалась монотонная сходимость критических волновых чисел по параметрам ограничения n (число элементов ряда, определяющего матричные элементы) и N (порядок приближения метода). Величины, полученные в третьем и четвертом приближении метода, совпадали с точностью не менее 10^-5. При изменении числа элементов ряда n и при фиксированном приближении N третий знак после запятой стабилизировался уже при n=100. Максимальная "несшиваемость" компонент полей на линиях раздела частичных областей составила 1.2%, при этом почти на всем интервале "сшивания" полей несовпадение было меньше 1%.

Получены зависимости нормированных критических волновых чисел Н- и Е-волн 4-х гребневого прямоугольного волновода от величин его выступов, в частности - для двух низших Н-волн. Эти критические волновые числа в основном определяют ширину рабочей полосы частот одномодового режима. Отмечена замена первой волны на вторую при определенных размерах выступов волновода. Для нормированных критических волновых чисел первых Н- и Е-волн всех типов квадратного 4-х гребневого волновода установлено, что с увеличением размеров квадратных выступов критические волновые числа для всех типов Н-волн монотонно убывают, а для Е-волн - возрастают. Причем полоса частот для одномодового режима плавно сужается при увеличении выступов волновода.

Получены также картины распределения поперечных компонент полей Н- и Е-волн по поперечному сечению 4-х гребневого прямоугольного волновода.

Приведенные в работе данные позволяют судить о характере электромагнитных полей рассмотренного типа волноводов и могут быть использованы при создании АР, в частности, для определения оптимальных по согласованию параметров поперечного сечения излучателей.