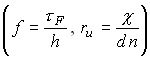|
Задача о разрушении столба смога Стерлитамакский государственный педагогический институт Научный руководитель: Шагапов Владик Шайхулагзамович, член-корр. АН РБ, профессор, доктор физико-математических наук В настоящей работе разрушение столба тяжелых выбросов отрицательной плавучести (плотность смеси больше плотности атмосферного воздуха) изучается на основе математической модели, построенной аналогично теории мелкой воды. При математическом описании процесса, были приняты следующие предположения: ветер отсутствует; распространение выбросов происходит вдоль горизонтальной поверхности. Учитывая принятые выше допущения, запишем уравнения сохранения массы и импульсов, а также уравнения сохранения для газовой фазы в квазиодномерном приближении
здесь u - скорость, h- высота;Уравнение состояния имеет вид:
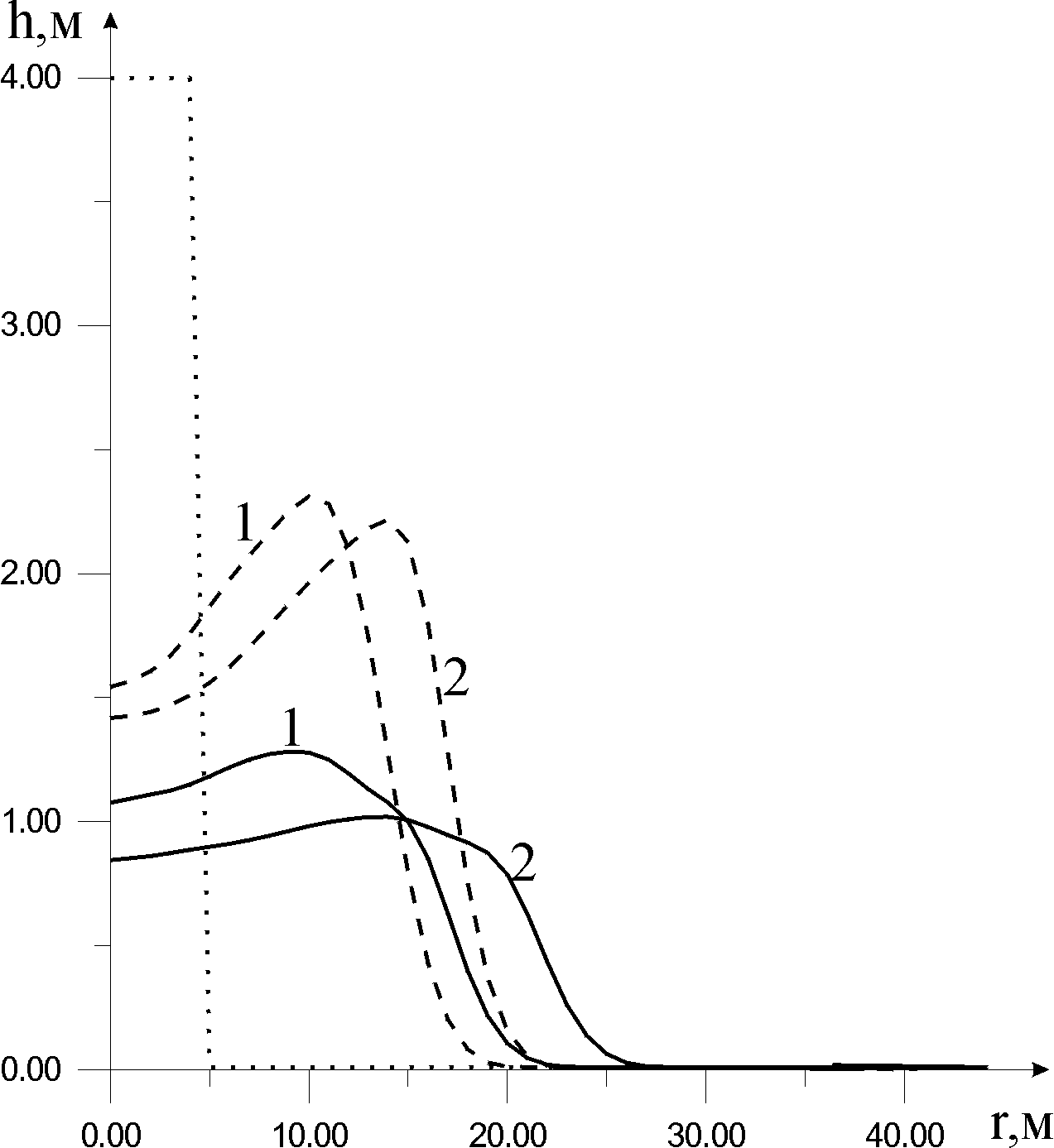
При растекании смога возможны две ситуации. Первая ситуация может возникнуть, когда высота смога ниже уровня наземных объектов. В этой ситуации преобладает сила сопротивления
d - где характерный диаметр деревьев, n-число деревьев нв единицу площади. Рассмотрим задачу о разрушении столба смога, образовавшегося после взрыва. Будем полагать, что после взрыва образовался столб смога шириной 2r0 и высотой h0. То есть начальные и граничные условия можно записать следующим образом
Начальная скорость смога считается нулевой, т.е.
Рис.1 На рис. 1 приведены результаты расчета для разных промежутков времени. В качестве начальных значений принималось |
| (c) АСФ России, 2001 |
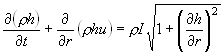 (1)
(1)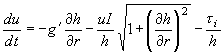 (2)
(2)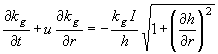 (3)
(3)