Численная корректировка сигналов в приборах с известной аппаратной функцией
Ласкин Виктор Александрович
Санкт-Петербургский государственный университет
Научный руководитель: Свентицкая Ирина Николаевна, кандидат физико-математических наук
В настоящее время в различных отраслях техники и в быту широко используются разнообразные оптические приборы с различными типами преобразования аналоговых сигналов. При этих преобразованиях всегда существуют искажения реальных исследуемых входных сигналов. Такие искажения не следует рассматривать только как аддитивный шум. Изменения структур входных сигналов могут происходить из-за несовершенства характеристик элементной базы прибора, что может быть охарактеризовано аппаратной функцией. В большинстве случаев указанными факторами пренебречь нельзя, и возникает задача восстановления исследуемых сигналов из искаженных. Эта практическая задача в зависимости от объекта исследования и сложности прибора может представлять значительную проблему.
Решена задача восстановления сигнала на входе по известному сигналу на выходе и аппаратной функции прибора. В работе изложен более быстрый и более устойчивый к шумам, в сопоставлении с распространенными в настоящее время, метод решения задачи.
Пусть функция рассеяния бесконечно узкого линейного источника (аппаратная функция K(x)) в некоем оптическом приборе задана. На вход прибора поступает исследуемый неизвестный сигнал (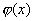 ). На выходе получаем искаженный сигнал (f(x)). Данная задача сводится к решению интегрального уравнения Фредгольма типа свертки: ). На выходе получаем искаженный сигнал (f(x)). Данная задача сводится к решению интегрального уравнения Фредгольма типа свертки:
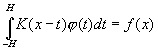 . (1) . (1)
В операторной форме (1) запишется как:
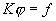 . (2) . (2)
Здесь физически оправдано считать функции 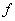 и и 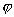 принадлежащими пространству принадлежащими пространству 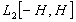 , а интегральный оператор , а интегральный оператор 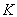 вполне непрерывным в вполне непрерывным в 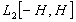 , что обусловлено физической природой гладкой функции рассеяния , что обусловлено физической природой гладкой функции рассеяния 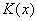 . Решение операторного уравнения (2) требует обратного отображения . Решение операторного уравнения (2) требует обратного отображения 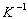 . Оно неустойчиво и данная задача считается математически некорректной. Сложность восстановления . Оно неустойчиво и данная задача считается математически некорректной. Сложность восстановления 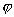 в том, что сколь угодно малые погрешности в том, что сколь угодно малые погрешности 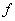 вызывают сколь угодно большие ошибки определения вызывают сколь угодно большие ошибки определения 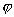 . Поэтому необходимо построить регуляризирующий алгоритм, учитывающий физическую природу явлений. . Поэтому необходимо построить регуляризирующий алгоритм, учитывающий физическую природу явлений.
Было получено искомое приближенное решение в виде ряда Фурье по системе собственных функций ядра интегрального уравнения:
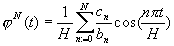 . (3) . (3)
где  - это коэффициенты в разложении в ряды Фурье известных функций. - это коэффициенты в разложении в ряды Фурье известных функций.
Регуляризирующую роль в данном алгоритме играет выбор 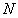 - числа гармоник, приближающих решение. Критерием оптимальности выбора - числа гармоник, приближающих решение. Критерием оптимальности выбора 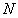 практически удобно принять достижение минимума значения функции практически удобно принять достижение минимума значения функции 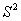 :
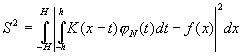 . (4) . (4)
Для эффективного изучения алгоритма, обладающего различной степенью устойчивости по отношению к различным классами функций и видам шумов, он был реализован на ЭВМ. Разработан пакет программ. Пакет позволил исследовать конкретные классы функций на применимость данного алгоритма, исследовать устойчивость данного алгоритма к различным видам шумов. Проведено многократное тестирование алгоритма. Была реализована программа для численной корректировки искаженных фотографий, которая является наилучшей практической иллюстрацией данного метода.
По итогам работы можно сделать следующие выводы.
- Данный алгоритм удобен в реализации на компьютере и позволяет быстро получать приближенное восстановление искаженного сигнала.
- Применение разработанного программного комплекса позволяет исследовать и повышать устойчивость решения в зависимости от количества узлов, числа членов ряда Фурье, характеристик шума.
- Программа для численной корректировки фотографий является практическим результатом данной работы.
- Использование БПФ позволило фантастически сократить время вычислений
.
Использование теоремы Котельникова позволило доказать возможность восстановления дискретной информации.
Изучена связь с распространенными фильтрами для коррекции изображений в графических редакторах (Blur, Sharpen, :) и возможность их обращения. Показано их несовершенство при обладании информацией об аппаратной функции.
Выявлена возможность практически полной коррекции дискретных данных без фильтрации их спектров при некоторых аппаратных функциях.
В данной задаче предполагается проводить как экспериментальную регуляризацию в различных условиях при разных характеристиках преобразующих приборов, так и теоретические оценки погрешности решения в различных формах и пространствах, что предполагается изучать впредь.
Возможности регуляризирующего алгоритма не ограничиваются приведенными результатами. В частности, планируется исследование неизопланатических приборов, а также проведение полного анализа устойчивости алгоритма в зависимости от характеристик шума.
|
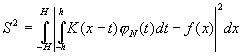 . (4)
. (4)