ВНКСФ7: Черёмухин Евгений Александрович: Применение теории измерительно-вычислительных систем для определения параметров пучка РЭМ

Применение теории измерительно-вычислительных систем для определения параметров пучка РЭМ

Черёмухин Евгений Александрович
Московский государственный университет им. М.В. Ломоносова

Научный руководитель: Грачёв Евгений Александрович, Канд. технич. наук

Одной из проблем, возникающих при работе, с растровым электронным микроскопом (РЭМ), является контроль качества используемого для сканирования электронного пучка. Как известно, разрешение РЭМ напрямую зависит от диаметра сфокусированного на образце пучка, поэтому разработка точных методов определения диаметра и других параметров электронного пучка является актуальной на сегодняшний день. Одним из основных методов определения диаметра пучка является метод кривых набегания [1]. Суть его в сканировании пучком края непрозрачной для излучения диафрагмы. Ток пучка, не задержанный диафрагмой, регистрируется при помощи цилиндра Фарадея и образует кривую набегания. Измерение диаметра пучка традиционным способом по падению тока кривой набегания обладает тем недостатком, что нет четкого критерия для всех исследователей определять диаметр однозначно. Поэтому задача измерения диаметра, в общем случае, сводится к определению плотности тока пучка в его сечении по множеству кривых набегания. Если известна математическая модель формирования кривых набегания, то оценить распределение плотности тока можно с помощью методов теории измерительно-вычислительных систем (ИВС) [2]. Эта задача решается путем математического преобразования (редукции) множества кривых набегания к виду, какой он имел бы при использовании "идеального" детектора, регистрирующего непосредственно распределение плотности тока пучка.

Распределением плотности тока пучка в сечении назовем квадратично-интегрируемую функцию , заданную на некотором подмножестве плоскости сечения пучка . Результат регистрации множества кривых набегания на цилиндре Фарадея имеет вид:

, (1)

где - множество кривых набегания для различных направлений сканирования, искаженных шумом системы регистрации тока набегания, на вход которой подано распределение плотности тока пучка для заданного сечения. Априори не делается никаких предположений о распределении . Корреляционная матрица шума цилиндра Фарадея предполагается известной и считается, что она не вырождена. Теперь рассмотрим линейное преобразование , при котором (1) запишется как

. (2)

Оператор определяет идеальный измерительный прибор, в нашем случае это детектор, непосредственно регистрирующий распределение плотности тока пучка. Цель преобразования получить наиболее точный синтез . Величина

(3)

определяет меру близости прибора к и является критерием качества синтеза .

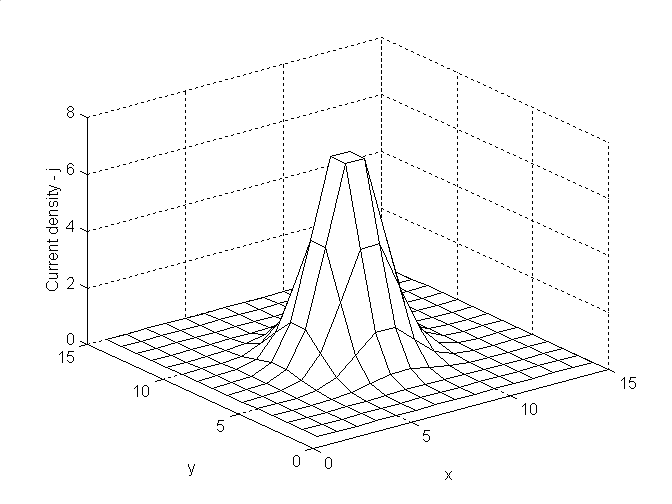
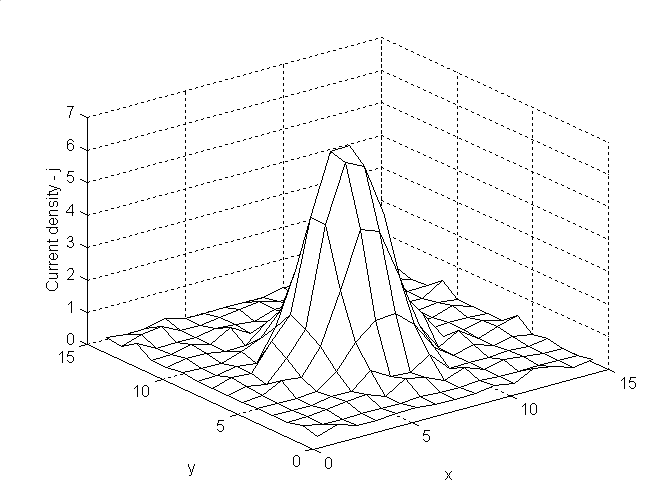
Таким образом наша задача сводится к нахождению оператора из условия минимума при заданном ограничении на уровень шума , то есть к решению вариационной задачи:

(4)

Решение задачи (4) подробно рассматривается в работах [2-3]. Простейший результат моделирования можно посмотреть на рис.1. В качестве модельного пучка был взят пучок с гауссовым распределением, который, как правило, используется в РЭМ

Рис 1. Модельное распределение плотности тока (слева) и восстановленное по кривым набегания распределение плотности тока пучка (справа). Уровень шума системы регистрации тока набегания - 1%.

В процессе работы на основе модели взаимодействия электронов с веществом [4] была построена модель получения кривых набегания с учетом взаимодействия электронов пучка с краем ножевой диафрагмы. При этом оказалось, что измерение диаметра пучка непосредственно по кривой набегания дает существенно завышенный результат. Применение методов теории ИВС позволяет учесть и этот эффект.

Список литературы:

[1] Грачёв Е.А., Кабанов А.Н., Кафафов А.А, Стахневич В.В. "Измерение параметров потока излучения методом диафрагм". // Оптико-механическая промышленность 1977, №10.

[2] Чуличков А.И. "Основы теории измерительно-вычислительных систем сверхвысокого разрешения (линейные стохастические измерительно-вычислительные системы)" // Издательство ТГТУ, 2000.

[3] Пытьев Ю.П. "Методы анализа и интерпретации эксперимента" // М.:Изд-во Московского университета,1990.
[4] Babin S., Borisov S., Grachev E., Shiriaev A. "An advanced Monte Carlo model of electron scattering in EBL involving fast secondary and true secondary electrons" // EIL-14P. Micro-and-Nano Engineering 2000. Jena, Germany. September 2000.