Стохастическая динамика релятивистского электрона в поле верхнегибридной волны и постоянном магнитном поле
Нагорных Елена Александровна
Алтайский государственный университет

Научный руководитель: Климов Олег Викторович, Кандидат физико-математических наук
Соавторы: Климов Олег Викторович, Тельнихин Александр Анатольевич

В связи с проблемами нагрева плазмы, ускорения частиц, происхождением космических лучей, представляет большой интерес задача о движении заряженной частицы в поле плазменных волн и магнитном поле.

Рассмотрим движение релятивистской заряженной частицы в постоянном магнитном поле | | z, перпендикулярнокоторому, вдоль распространяется электромагнитная волна с частотой w и волновым числом k. Векторный потенциал выберем в виде: и скалярный потенциал имеет вид . Тогда Гамильтониан Н заряженной частицы в данных условиях принимает вид:

, (1)

где , m - масса электрона, с - скорость света, p - импульс частицы.

Задача в общем виде не интегрируется, поэтому для решения удобно перейти к переменным действие-угол. В дальнейшем анализ проведем для частиц, обладающих достаточно большой энергией В этом случае можно воспользоваться теорией возмущений, учтя нелинейный резонанс.

Из проведенного анализа динамики частицы вытекают следующие результаты.

Движение частицы в поле волнового пакета и магнитном поле является причиной возникновения большого числа гармоник с частотами, кратными циклотронной частоте . В результате перекрытия нелинейных резонансов в детерминированной системе возникает хаос (сложное движение со стохастической динамикой).

Исследование движения частицы с помощью диффузионного уравнения показали, что средняя энергия частиц при растет по закону , что совпадает с [1].

В случае темп прироста энергии значительно выше

В фазовом пространстве системы динамический хаос проявляется в макроскопическом эффекте - ускорении частиц в область высоких энергий, причем более эффективно ускоряются частицы, резонансно взаимодействующие с потенциальным полем волны.

Получены отображения, описывающее динамику в векторном и скалярном поле волны. Проведены исследования диссипативных отображений в двух случаях: когда существенны лишь тормозные потери - случай слабой диссипации и в случае синхротронного излучения.

Рассмотрим одно из отображений.

Релятивистская заряженная частица теряет энергию за счет излучения электромагнитных волн. В случае синхротронного излучения, отображение, описывающее динамику частицы в скалярном поле волны, имеет вид:

(2)

где

Фазовый объем системы уменьшается с характерным временем сжатия где =найдено из условия критерия стохастичности. В системе развивается локальная неустойчивость. Сочетание глобального сжатия с локальной неустойчивостью является условием возникновения сложного стохастического движения. Результаты компьютерного моделирования типичного поведения системы (2) в области стохастичности показаны на (рис. 1).

рис.1. Фазовый портрет диссипативного отображения при Начальные значения

рис.2. Зависимость в полулогарифмическом масштабе.

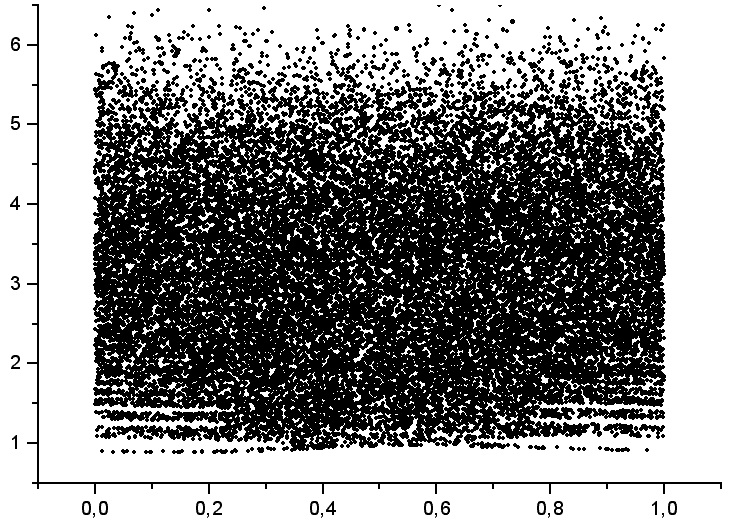
Характерной особенностью является наличие верхней границы по энергии для ускорения частиц

(3)

Результаты численного эксперимента показывают (рис. 2), что зависимость с хорошей точностью описывается выражением (3).

 

Список литературы:

[1] Заславский Г.М., Сагдеев Р.З., ЖЭТФ, т.93, вып.3(9) (1987)

[2] Кронберг Е.А., Нагорных А.О., Тельнихин А.А., Известия АГУ, 1(6)(1998)

(c) АСФ России, 2001