Моделирование пульсаций скорости и их пространственного масштаба при изотропной турбулентности
Студенок Сергей Игоревич
Уральский государственный университет
Научный руководитель: Быстрай Геннадий Павлович, кандидат физ-мат наук
Одной из принципиальных задач в решении проблемы развитой турбулентности является установление нелинейной взаимозависимости пространственных и скоростных характеристик турбулентных пульсаций.
Разложив мгновенные скорость, давление и силу в гиперболическом уравнении Навье - Стокса [1] для вязкой несжимаемой жидкости на осредненные и пульсационные составляющие и учтя справедливость этого уравнения для осредненных (стационарных) величин, выделяется его нестационарная часть. При переходе к изотропным пульсациям принимается, что основное течение одномерно, а его градиент всюду равен нулю. Тогда гиперболическое уравнение Навье - Стокса для пульсационной составляющей скорости h трехмерного изотропного турбулентного течения в приведенном виде имеет вид:
 + + +3h +3h  = = - - + +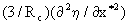 , (1) , (1)
где h є h *є h /Vc, x *є x/x c - приведенная пространственная координата вдоль направления основного течения V? ; t є t *є t /t0 - приведенное время релаксации, которое оказывает дестабилизирующее воздействие на течение жидкости; tє  є t/t0 - приведенное время (t0=x c/Vc); Rc=Vcx c/n - критическое число Рейнольдса перехода к турбулентности, r ,n - плотность и кинематическая вязкость жидкости. Приведенные величины p*`є p`/r Vc2, f*`є f`x c/Vc2 являются функциями масштабных характеристик: пространственного размера (x c) и скорости (Vc). є t/t0 - приведенное время (t0=x c/Vc); Rc=Vcx c/n - критическое число Рейнольдса перехода к турбулентности, r ,n - плотность и кинематическая вязкость жидкости. Приведенные величины p*`є p`/r Vc2, f*`є f`x c/Vc2 являются функциями масштабных характеристик: пространственного размера (x c) и скорости (Vc).
В общем случае рассматривается следующая качественная математическая модель, которая предполагается в определенном приближении изоморфной уравнению Навье - Стокса (1):
3h  є h 3+ є h 3+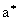 h + h + , , 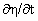 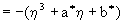 , (2), (3) , (2), (3)
где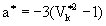 и и  -параметры качественной модели; -параметры качественной модели; 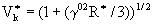 - некоторая средняя приведенная скорость; 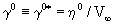 - задаваемая интенсивность изотропных стационарных пульсаций h 0, которая связана с параметром - задаваемая интенсивность изотропных стационарных пульсаций h 0, которая связана с параметром 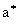 cоотношением: cоотношением: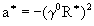 ; ;  , ,  ; ;  - приведенное число Рейнольдса, R=V? x c/n , - приведенное число Рейнольдса, R=V? x c/n ,  . Из свойств изотропности пульсаций следует, что величина . Из свойств изотропности пульсаций следует, что величина 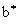 =0. Совместность уравнений (2) и (3) требует, чтобы были выполнены следующие соотношения: =0. Совместность уравнений (2) и (3) требует, чтобы были выполнены следующие соотношения:  , ,  , где , где  - новый параметр задачи. В результате такого моделирования приходим к следующим качественным нелинейным уравнениям с разделяющимися переменными: - новый параметр задачи. В результате такого моделирования приходим к следующим качественным нелинейным уравнениям с разделяющимися переменными:
 , , 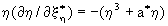 ; (4),(5) ; (4),(5)
где  - восприимчивость. - восприимчивость.
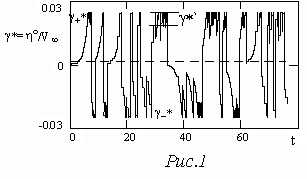
Установлено, что при численном решении уравнения (4) и временном шаге h є D tR 0 t TR t 0=-1/2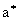 возникают детерминированные хаотические решения h (t) - пульсации скорости, выраженые при анализе в долях от средней приведенной скорости потока в виде возникают детерминированные хаотические решения h (t) - пульсации скорости, выраженые при анализе в долях от средней приведенной скорости потока в виде  =h (t)/ =h (t)/ =h (t)/ =h (t)/ =h 0/V (рис.1) ( =h 0/V (рис.1) (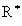 =44.44, g 0=2.498%, t T=0.4043365, h=0.005054206, h {0}=0.01). Пунктирной линией указаны средние значения на рассматриваемом интервале времени, близкие к нулевым, что характерно для изотропной турбулентности. =44.44, g 0=2.498%, t T=0.4043365, h=0.005054206, h {0}=0.01). Пунктирной линией указаны средние значения на рассматриваемом интервале времени, близкие к нулевым, что характерно для изотропной турбулентности.
Из рисунка видно, что в крупномасштабной области характеристик 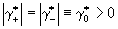 сосредоточены мелкомасштабные пульсации со скоростями сосредоточены мелкомасштабные пульсации со скоростями  , в которых происходит "сброс" кинетической энергии жидкости и превращение ее в тепло. , в которых происходит "сброс" кинетической энергии жидкости и превращение ее в тепло.
После интегрирования уравнения (5), связывающего пульсации скорости h с пространственной координатой 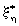 , при , при 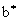 =0 и граничными условиями h =0, =0 и граничными условиями h =0, 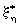 =0, получаем зависимость =0, получаем зависимость  = =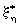 / /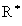 от пульсаций скорости h : от пульсаций скорости h :
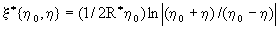 , ,  . .
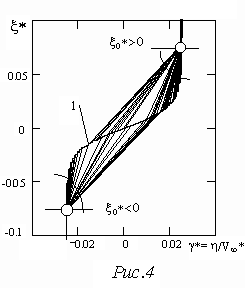
На (рис.2) приведена получаемая из строгих решений корреляция между хаотическими значениями пространственного размера пульсаций  и пульсаций скорости и пульсаций скорости  . Автоматически получаемое стационарное решение (кривая1) может быть сравнено с законом Колмогорова - Обухова . Автоматически получаемое стационарное решение (кривая1) может быть сравнено с законом Колмогорова - Обухова  ~ 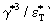 при постоянной величине диссипации энергии при постоянной величине диссипации энергии 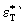 =const и показывает в первом приближении на их удовлетворительное соответствие. Как в стационарной, так и в нестационарной задачах при =const и показывает в первом приближении на их удовлетворительное соответствие. Как в стационарной, так и в нестационарной задачах при 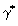 R R  (h R h 0) возникают логарифмические расходимости, обуславливающие резкие, но конечные скачки пространственных характеристик. Тем не менее, в рамках динамической задачи для хаотического параметра порядка создается возможность на основе численных расчетов определять (h R h 0) возникают логарифмические расходимости, обуславливающие резкие, но конечные скачки пространственных характеристик. Тем не менее, в рамках динамической задачи для хаотического параметра порядка создается возможность на основе численных расчетов определять  , как некоторый характерный масштаб пространственных пульсаций для любого числа Рейнольдса, в том числе и при , как некоторый характерный масштаб пространственных пульсаций для любого числа Рейнольдса, в том числе и при  R ? , который удовлетворяет условию инерционного интервала R ? , который удовлетворяет условию инерционного интервала 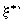 << <<  <<1. <<1.
1. Алексеев Б.В. Физические основы обобщенной больцмановской кинетической теории газов // УФН. 2000. Т. 170. №6. C. 649-679.
|