ВНКСФ7: Дюжева Марина Сергеевна: Изменение вида кривой, описывающей рассеивающую способность сферических коллоидных частиц, при переходе от монодисперсных образцов к полидисперсным

Изменение вида кривой, описывающей рассеивающую способность сферических коллоидных частиц, при переходе от монодисперсных образцов к полидисперсным

Дюжева Марина Сергеевна
Санкт-Петербургский государственный морской технический университет

Научный руководитель: Клюбин Владимир Владимирович, Доктор физико-математических наук, профессор

Процесс определения размеров коллоидных частиц с использованием метода динамического светорассеяния (ДС) состоит в измерении спектральных (или корреляционных) характеристик релеевской компоненты рассеянного света и пересчете их в концентрацию и гидродинамические диаметры рассеивающих частиц. Интенсивность рассеянного света I(n, r) пропорциональна числу рассеивателей N и величине

, (1)

которая называется рассеивающей способностью коллоидных частиц. Здесь r - радиус, а f(r) форм-фактор частицы, который сложным образом зависит от размера рассеивателей.

Чтобы подробнее исследовать зависимость рассеивающей способности от размеров частиц мы провели расчеты R(r) с помощью компьютерной программы MATHCAD, считая, что рассеяние происходит при следующих условиях: угол рассеяния равен , длина волны l = 632,8 нм, показатель преломления дисперсионной среды n = 1.333, а радиусы частиц меняются от 1 нм до 7 мкм. Для релеевской области размеров рассеивающая способность частиц представляет собой монотонную степенную функцию , а для крупных частиц (по сравнению с длиной волны) функция R(r) имеет вид осциллирующей кривой (рис.1, кривая 1), которая для некоторых размеров обращается в ноль. При вычислении концентрации частиц в этих точках можно получить бесконечно большие значения, что нелепо с точки зрения здравого смысла. Чтобы обойти эту ситуацию, при обработке экспериментальных данных в приборах, основанных на методе ДС, рассеивающая способность крупных частиц считается пропорциональной - эта линия соответствует средним значениям осциллирующей кривой.

Приведенные выше рассуждения и формулы справедливы в том случае, когда исследуемая дисперсия состоит из частиц одного размера, то есть для монодисперсных образцов. Реальные же коллоиды всегда полидисперсны. В этом случае, специальные алгоритмы обработки данных ДС позволяют получить распределение частиц по размерам, раскладывая измеренный релеевский спектр рассеянного света на отдельные компоненты. В каждой из компонент содержится рассеяние от частиц близких, но не одинаковых, размеров. В связи с этим рассеивающая способность частиц выделенной фракции (одной компоненты распределения) будет отличаться от функции (1). В данной работе мы попытались разобраться в том, как изменится при этом вид функции, описывающей рассеивающую способность R(r).

Учет рассеяния от многих частиц, входящих в данную фракцию, приводит к тому, что рассеивающую способность необходимо определять с помощью выражения:

, (2)

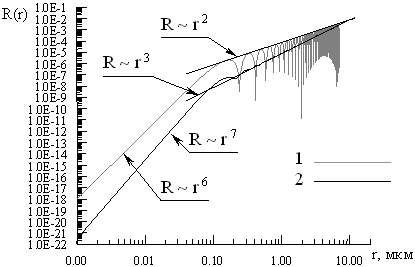
в котором величина B(r) представляет собой функцию распределения частиц по размерам в пределах данной выделенной фракции. В пределах конкретной фракции распределение части по размерам может изменяться по различному закону. Оно может нарастать, как это имеет место для фракций, расположенных слева от максимума распределения частиц по размерам N(r), либо убывать по линейному закону, для фракций, расположенных справа от максимума распределения N(r). Вблизи максимума кривой N(r) величина B(r) может изменяться куполообразным образом либо оставаться постоянной. Мы выполнили расчеты рассеивающей способности R(r), используя все перечисленные зависимости B(r).

Мы показали, что степенные зависимости, которыми можно описать рассеивающие способности монодисперсных и полидисперсных образцов совпадают лишь в том случае, если программа обработки данных спектроскопии оптического смешения построена таким образом, что шкала размеров частиц является линейной. Но приборы, наиболее часто используемые для измерений с помощью метода ДС, содержат алгоритм, который работает с нелинейной шкалой размеров частиц. Дело в том, что в методе ДС распределение числа рассеивающих частиц по размерам N(r) является вторичным, так как в приборах непосредственно измеряется распределение I(Г) интенсивностей компонент рассеянного света по величине полуширины релеевского света Г. При пересчете равномерный шаг по шкале Г трансформируется в неравномерный (возрастающий) шаг по шкале размеров. А вид кривой R(r), при переходе от монодисперсных к полидисперсным образцам, существенно меняется. Расчеты показывают, что, вне зависимости от вида распределения B(r), в релеевской области эту кривую можно аппроксимировать седьмой степенью размера рассеивателей, а в области больших, по сравнению с длиной волны, частиц - третьей степенью (рис.1, кривая 2).

рис. 1