|
Фазовые скорости упругих волн в тонком изотропном цилиндрическом стержне, строгое решение Санкт-Петербургский государственный морской технический университет Научный руководитель: Клещев Александр Александрович, Кандидат технических наук В данной работе вслед за [1], [2] изучаются фазовые скорости упругих волн в изотропном цилиндрическом стержне радиуса а. Обратимся к строгому решению задачи. Плотность материала стержня r , коэффициенты Ламе - l и m . Вектор смещения стержня
По теореме Гельмгольца вектор смещения
Векторная функция
где: w - круговая частота гармонических колебаний, k =(w /с2) - волновое число поперечной волны в материале стержня; с2 - скорость поперечной волны;Цилиндрические компоненты А r, Аj , Аz функции
Потенциалы F , U, V разложим по собственным функциям скалярного уравнения Гельмгольца. Неизвестные коэффициенты этих разложений определяются из граничных условий на поверхности стержня: отсутствие нормального и касательных напряжений:
Подставляя разложения потенциалов F , U, V в граничные условия (7)ё (9), приходим к определителю 3-го порядка. Если радиус стержня а=1.0, то уравнение для волновых чисел k трехмерных изгибных волн принимает вид:
где: h ў =(h2-k2)?; k ў =(k 2-k2)?; h - волновое число продольной волны в материале; Jm(hў ) - цилиндрическая функция Бесселя.Характеристические уравнения для осесимметричных продольной и крутильной волн даны в [3]. На основе уравнения для крутильной волны в изотропном стержне были выполнены расчеты фазовых скоростей первых пяти мод для стального стержня с радиусом а=1.0. Результаты этих расчетов представлены на рисунке, при этом используются следующие обозначения: l кр - длина крутильной волны, прямая 1 (нулевая мода) соответствует постоянной скорости, равной скорости поперечной волны с2.
Список литературы: |
| (c) АСФ России, 2001 |
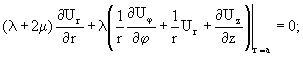 (7)
(7)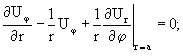 (8)
(8)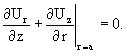 (9)
(9)
