Приложение теории катастроф к описанию упругопластической деформации материалов. Изотропное тело.
Тихомирова Ирина Сергеевна
Ивановский государственный университет
Научный руководитель: Лев Николаевич Маурин, доктор физико-математических наук
В процессе деформации материал может находиться как в устойчивом ( ), так и в неустойчивом ( ), так и в неустойчивом ( ) состоянии. Наиболее известным примером неустойчивости пластической деформации является скачкообразная деформация при низких температурах. При этом на кривой деформации наблюдаются срывы. Другим примером является эффект Портевина-Ле-Шателье (здесь также неравномерный характер изменения скорости деформации проявляется на кривых ) состоянии. Наиболее известным примером неустойчивости пластической деформации является скачкообразная деформация при низких температурах. При этом на кривой деформации наблюдаются срывы. Другим примером является эффект Портевина-Ле-Шателье (здесь также неравномерный характер изменения скорости деформации проявляется на кривых 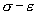 в виде повторяющихся скачков текучести). В обоих случаях на появление, форму и глубину скачков оказывают влияние различные факторы, как внешние, так и внутренние. в виде повторяющихся скачков текучести). В обоих случаях на появление, форму и глубину скачков оказывают влияние различные факторы, как внешние, так и внутренние.
Целью настоящей работы является построение модели, описывающей в рамках макроскопического подхода скачкообразную деформацию материалов. Здесь представлена наиболее простая модель (первый шаг), не учитывающая влияние среды и изменения в составе материала (в частности влияние примесей).
В основе нашего рассуждения лежит предположение, что в процессе деформации происходит смена устойчивости. Так переход из упругого состояния в пластическое можно рассматривать как смену одного устойчивого состояния (упругого) другим устойчивым состоянием (пластическим). При дальнейшем нагружении (активное нагружение) опять может произойти потеря устойчивости (если 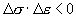 ), следствием которой является переход из пластического состояния в упругое. Таким образом, в данной модели мы предполагаем, что в какой-то момент пластическая разгрузка сменяется упругим нагружением, затем опять следует пластический срыв и упругое нагружение и т. д. Следует отметить, что в данной работе мы не рассматриваем упрочняющиеся среды, то есть, моделируем поведение идеально упругопластического материала. Кроме того, рассматривается случай одномерного статического нагружения и не учитывается эффект Баушингера. ), следствием которой является переход из пластического состояния в упругое. Таким образом, в данной модели мы предполагаем, что в какой-то момент пластическая разгрузка сменяется упругим нагружением, затем опять следует пластический срыв и упругое нагружение и т. д. Следует отметить, что в данной работе мы не рассматриваем упрочняющиеся среды, то есть, моделируем поведение идеально упругопластического материала. Кроме того, рассматривается случай одномерного статического нагружения и не учитывается эффект Баушингера.
Основная идея работы состоит в привлечении теории катастроф, согласно которой нужно построить функцию состояния 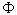 . Мы прелагаем записать ее в виде катастрофы сборки . Мы прелагаем записать ее в виде катастрофы сборки
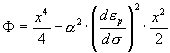 , (1) , (1)
где 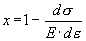 - отклонение от прямой, описываемой законом Гука, - отклонение от прямой, описываемой законом Гука, 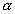 - параметр, - параметр, 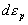 - приращение пластической деформации, - приращение пластической деформации, 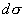 - приращение напряжения, - приращение напряжения, 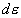 - приращение полной деформации, причем - приращение полной деформации, причем 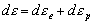 , где , где  - приращение упругой составляющей деформации. Из вида функции состояния ясно, что мы описываем изотропные материалы и не учитываем эффект Баушингера. - приращение упругой составляющей деформации. Из вида функции состояния ясно, что мы описываем изотропные материалы и не учитываем эффект Баушингера.
Исследуя 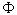 на устойчивость, нетрудно найти, что существуют следующие решения: на устойчивость, нетрудно найти, что существуют следующие решения:
 (2) (2)
- устойчиво на участке упругой деформации и неустойчиво при пластической деформации;
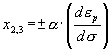 (3) (3)
- устойчиво на участке пластической деформации и совпадает с (2) (т.е. неустойчиво), если тело ведет себя как упругое.
Из (2) следует, что 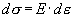 , то есть здесь выполняется закон Гука (дифференциальная форма). Выражая из (3) , то есть здесь выполняется закон Гука (дифференциальная форма). Выражая из (3) 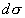 , находим , находим 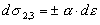 . Таким образом, наше решение в пластической области дает две устойчивые ветви - восходящую и нисходящую. Для однозначного выбора ветви, которая описывает деформационную зависимость, необходимо учесть факторы, влияющие на процесс деформации, что является следующим шагом в уточнении модели, и в данной работе не рассматривается. Здесь необходимо отметить, что параметр . Таким образом, наше решение в пластической области дает две устойчивые ветви - восходящую и нисходящую. Для однозначного выбора ветви, которая описывает деформационную зависимость, необходимо учесть факторы, влияющие на процесс деформации, что является следующим шагом в уточнении модели, и в данной работе не рассматривается. Здесь необходимо отметить, что параметр a не постоянная величина, а функция, зависящая от накопленной пластической деформации 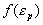 или от полной деформации или от полной деформации 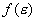 , достигнутой к данному моменту нагружения. Данная функция подлежит определению в ходе эксперимента. , достигнутой к данному моменту нагружения. Данная функция подлежит определению в ходе эксперимента.
Из равенств (2) и (3) ясно, что переход из упругой области в пластическую происходит плавно (непрерывно). Рассмотрим теперь, как будет вести себя модель, если тело начинают разгружать. В этом случае 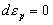 и функция состояния примет вид и функция состояния примет вид 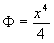 , а единственно существующим устойчивым решением будет , а единственно существующим устойчивым решением будет 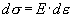 (закон Гука в дифференциальной форме) или (закон Гука в дифференциальной форме) или 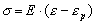 , где , где 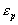 - величина остаточной (пластической) деформации, накопленной к моменту начала разгрузки. - величина остаточной (пластической) деформации, накопленной к моменту начала разгрузки.
В заключение отметим, что если при пластической деформации тело разупрочняется (в нашем случае 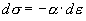 ), то параметр ), то параметр  должен вести себя таким образом, что при определенной деформации должен вести себя таким образом, что при определенной деформации 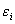 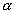 становится равным нулю, и, следовательно, при дальнейшем нагружении модель ведет себя как линейно упругое тело (т.е. подчиняется закону Гука). Значения становится равным нулю, и, следовательно, при дальнейшем нагружении модель ведет себя как линейно упругое тело (т.е. подчиняется закону Гука). Значения 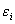 , при которых происходит смена закона деформирования (переход от пластического состояния к упругому), должны определяться экспериментально. , при которых происходит смена закона деформирования (переход от пластического состояния к упругому), должны определяться экспериментально.
Выводы:
- предложенная модель описывает упругое поведение материала, непрерывный переход из упругого состояния в пластическое и упругую разгрузку;
- получена аналитическая форма деформационной зависимости на участке пластической деформации.
|
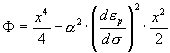 , (1)
, (1)