|
Природа спиновой релаксации в высокотемпературных сверхпроводниках Казанский государственный университет Научный руководитель: Кочелаев Борис Иванович, Доктор физ-мат наук Экспериментальные факты свидетельствуют о том, что спиновые корелляции играют большую роль в свойствах квазидвумерных допированных дырками окислов меди, являющихся высокотемпературными сверхпроводниками (ВТСП). Прямой метод исследования данной проблемы-это электронный парамагнитный резонанс (ЭПР). Однако многочисленные эксперименты показали отсутствие ЭПР-синала в ВТСП-материалах. Проблема отсутствия ЭПР-сигнала в сверхпроводящих купратах была объектом интенсивных теоретических и экспериментальных исследований. В частности, Чакраварти, Орбах [1] и Лазута [2] объясняли уширение линии при температурах ниже комнатной статическим взаимодействием Дзялошинского-Мориа. Они показали, что с понижением температуры ширина линии экспоненциально растет, что могло объяснить отсутствие сигнала ЭПР. Поэтому они решили, что ЭПР-сигнал должен наблюдаться при более высоких температурах. П. Симон и др. [3] пытались обнаружить ЭПР-сигнал при температурах вплоть до 1150K, но безуспешно. Очевидно, что отсутствие ЭПР-сигнала обусловлено другими причинами. Обнаруженный в недавних экспериментах [7] сильный изотопический эффект позволяет предположить важную роль колебаний решетки в механизме релаксации. Предположим, что взаимодействие между синовой системой ионов меди Cu 2+ и колебениями решетки осуществляется благодаря модуляции кристаллического электрического поля искажениями решетки и спин-орбитальным взаимодействием ионов меди. Для спиновой системы ионов меди нижним состоянием является Крамерсов дублет. Как известно, кристаллическое электрическое поле не может вызвать переходы в Крамерсовом дублете. К осовному состоянию d(x2-y2) изотропное обменное взаимодействие примешивает возбужденные состояния d(xz) и d(yz) группы Г5g. Согласно [4], это означает, что будут присутствовать только колебения типа Q4 и Q5, описывающие искажения, соответствующие наклонам апикальных ионов кислорода вокруг диагональной оси квадрата CuO4. Исходя из этих соображений в работе [5] был получен гамильтониан спин-решеточного взаимодействия следующего вида:
Здесь Для вычисления скорости спин-решеточной релаксации потребуются спиновые корелляционные функции, и здесь тоже возникают проблемы, так как в двумерных магнетиках очень велики спиновые флуктуации. Существующие методы, такие, как ренорм-группа или 1/N-метод очень сложны и громоздки. В настоящей работе используется подход, основанный на том, что исходное состояние неоднородно вследствие возникновения топологических возбуждений-скирмионов [6]. В этом подходе сильные флуктуации учитываются неоднородностью основного состояния, и спиновые корелляционные функции определяются спиновыми волнами на фоне этого неоднородного базиса.Скорость спин-решеточной релаксации была вычислена на основе факторизации 4-х спиновой корелляционной функции, а корелляционная функция колебаний решетки получена в гармоническом приближении. В результате было получено следующее выражение для скорости спин-решеточной релаксации:
Здесь М-масса кислорода,
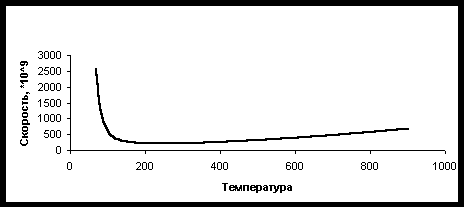
рис.1 Температурная зависимость скорости релаксации. Необходимо отметить пропорциональность скорости релаксации размеру скирмиона, что служит аналогом корелляционной длины. Температурная зависимость (см. рис1) немонотонна: скорость релаксации при температурах выше комнатной растет с ростом температуры почти линейно, также резко возрастает при низких температурах. Такая зависимость хорошо согласуется с экспериментом. Численная оценка скорости релаксации дает велечину порядка 10111/c. Такая большая величина (больше ларморовой частоты) может объяснить отсутствие ЭПР-сигнала в сверхпроводящих магнетиках и их родительских соединениях. Список публикаций: [1] S.Chakravarty and R.Orbach, Phys Rev. Lett. 64, 224 (1991). [2] A.V.Lazuta, Physica C 181, 127 (1991). [3] P.Simon et al., Phys Rev. B 48, 4216 (1993). [4] А.Абрагам, Б.Блини "ЭПР ионов переходных металлов" Москва, 1972г. [5] Kochelaev et al. J.Superconductivity, 12, 53 (1999). [6] Belov S.I. and Kochelaev B.I., Solid State Commun., 103, 249, (1997). [7] A. Shengelaya et al., accepted by Phys.Rev. |
(1)
означает сумму по ближайшим соседям в плоскости x-y, константы 
и G - соответственно константы спин-орбитального и орбитально-решеточного взаимодействия, 
- величина расщепления между основным и возбужденым орбитальными уровнями энергии. 
(2)
-частота решеточных колебаний, 
-размер скирмиона.
| (c) АСФ России, 2001 |