|
Применение четырехмерных представлений для индицирования гексагональных кристаллов Гродненский государственный университет Научный руководитель: Лиопо Валерий Александрович, д.ф.-м.н. Квадратичная форма гексагонального кристалла имеет вид
следовательно, в процессе индицирования рентгенограммы, включающей N рефлексов, надо определить 3N+2 неизвестных параметров. В работе [1] показано, что в четырехмерном пространстве гиперкубические решетки характеризуются группами точечной симметрии, подгруппами которых являются точечные группы гексагональных кристаллов. Другими словами гексагональная трехмерная решетка может рассматриваться как своеобразная проекция (или сечение) четырехмерной кубической решетки на трехмерное пространство. В этом случае гексагональные кристаллы можно индицировать по методике индицирования кубического кристалла.В идеальной гексагональной решетке отношение
или
где М-целое число. По теореме Лагранжа: любое целое число можно представить в виде суммы квадратов четырех целых чисел. Тогда формула (3) примет вид
где m,n,p,q-индексы плоскостей четырехмерной гиперкубической решетки. Следовательно, по отношениям обратных квадратов межплоскостных расстояний гексагонального кристалла определяются индексы m, n, p, q. Связь между индексами m, n, p, q и h, k, l однозначная и легко устанавливается при сравнении формул (4) и (3). Индицирование, выполненное нами на модельных объектах и реальных рентгенограммах различных гексагональных кристаллов. Нами установлено, что методика, описанная выше, может быть использована и в случае, когда
где n-число значений М (см. формулу (3)), у которых индексы имеют тип hk0. Затем необходимо найти значения
для которых индексы относятся к типу hkl (h и k могут быть равными 0). Следовательно, определяется среднее значение с (
где р - число значений М' (см. формулу (6)), у которых индексы имеют тип hkl. По параметрам Методика проверена на рентгенограммах нескольких десятков кристаллов. Во всех рассматриваемых случаях наблюдается полное совпадение рассчитанных индексов с базами данных. Список публикаций: [x] В.А. Лиопо. Гексагональная решетка в четырехмерном пространстве.// Весцi НАН РБ, сер.фiз-мат.навук 1999.-№1.-С.103-106. |
| (c) АСФ России, 2001 |
 , (1)
, (1) , (5)
, (5)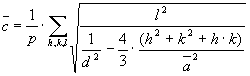 , (7)
, (7)