|
Полупространственные моменты в граничных задачах кинетической теории газов Самарский государственный университет Научный руководитель: Курочкин Виктор Иванович, д.ф.-м.н., проф. При течении газов и газовых смесей вблизи поверхности, а также в задачах теплообмена и испарения-конденсации, функция распределения частиц по скоростям вблизи поверхности (в так называемом слое Кнудсена) является, как правило, разрывной в пространстве скоростей. Для газа вблизи стенки роль числа Кнудсена играет отношение средней длины свободного пробега к расстоянию до стенки. При исследовании слоя толщиной в несколько длин свободного пробега число Кнудсена нельзя считать малым и предположения, лежащие в основе метода Чепмена-Энскога, перестают быть справедливыми. В ряде интересных случаев, в частности при рассмотрении медленных течений, функция распределения газовых молекул может слабо отличаться от максвелловской, и возможна линеаризация уравнения Больцмана. При решении линеаризованного стационарного кинетического уравнения в таких случаях функцию распределения представляют в виде ряда
где
где В настоящее время рассчитаны только несколько простых
интегральных скобок, содержащих Полученные скобки позволяют уточнить решение ряда задач с использованием точного выражения для интеграла столкновений. Были рассмотрены следующие задачи: 1. Задача Крамерса — задача о течении со скольжением, представляет собой течение Куэтта с одной стенкой расположенной на бесконечности, при отсутствии теплового потока. Вдали от поверхности стенки величина градиента массовой скорости потока газа считается постоянной и заданной. В качестве граничного условия на стенке принимается зеркально-диффузное отражение. На бесконечности функция распределения принимает вид распределения Чепмена-Энскога. Искомыми являются коэффициент изотермического скольжения2. Задача о тепловом скольжении — задача о движении газа,
находящегося в поле тангенциального к стенке градиента температуры. Значение
градиента температуры считается постоянным и заданным. В качестве граничного
условия на стенке принимается зеркально-диффузное отражение. На бесконечности
функция распределения принимает вид распределения Чепмена-Энскога. Искомыми
являются коэффициент теплового скольжения 3. Задача о температурном скачке. На стенке принимается
граничное условие диффузного отражения с коэффициентом аккомодации энергии.
Вдали от поверхности стенки величина градиента температуры считается постоянной
и заданной. На бесконечности функция распределения принимает вид распределения
Чепмена-Энскога. Искомыми являются коэффициент температурного скачка 4. Задача о слабом испарении. В задаче рассматриваются особенности слоя Кнудсена при испарении поверхности со слабой интенсивностью. Скорость истечения на внешней границе слоя Кнудсена считается постоянной и заданной. В качестве граничного условия на стенке принимается, что молекулы отражаются диффузно с температурой стенки. На внешней границе слоя функция распределения приобретает равновесный максвелловский вид. Искомыми являются профили концентрации и температуры в слое Кнудсена. Вышеприведенные задачи решались методом полупространственных моментов: функция распределения разлагалась по ортогональным полиномам скорости с коэффициентами зависящими от пространственных координат (1). Коэффициенты разложения находятся из системы обыкновенных дифференциальных уравнений, полученной из кинетического уравнения. Получены значения коэффициентов скольжения, коэффициента температурного скачка для потенциала твердых сфер и для степенного потенциала. Приведено сравнение результатов с другими работами, а для задачи Крамерса и с экспериментальными данными. |
| (c) АСФ России, 2001 |
 , (1)
, (1)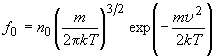 —
максвелловская функция, коэффициенты
—
максвелловская функция, коэффициенты