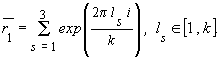Научный руководитель: Шипилин Николай Николаевич, д.с.-х.н.
Соавторы: Сергеев Михаил Анатольевич

В последние годы наука о самоорганизации выходит за рамки синергетики и высказывается мнение о необходимости учета геометрических свойств реального пространства [1]. Геометрический аспект, наряду с термодинамическим и информационным, становится одним из основных при моделировании процессов самоорганизации и особенно в биологическом морфогенезе. В отличие от евклидовой геометрии линейных и нелинейных событий эллиптическая геометрия Римана допускает процессы спирально-циклической самоорганизации [2]. Существует система координат в которой замкнутое эллиптическое пространство биобъекта обладает зональным строением. Такое строение пространства, независимо от заполнения его веществом, является заданной возможностью для развития спирально-циклических направленных форм движения. В ранних моделях морфогенеза основное внимание уделялось механизмам становления биохимического паттерна морфофункциональных модулей, а вопросы их пространственной геометрии оставались на втором плане. Зависимость латерального транспорта от общей гауссовской кривизны и другие проявления диссипативных структур позволили сформулировать новый класс моделей, основанный на положении о взаимообусловленности динамики и геометрической формы паттернов модулей. Изучению механизмов взаимообусловленной динамики паттернов модулей от внутренней и внешней их геометрии может способствовать моделирование самоорганизации двумерных (2D) каналов коллективного направленного переноса морфогенов. Предполагается, что необходимым условием морфогенеза является передача информации с помощью волн дифференцировки [3]. Представляется возможным с помощью эллиптической геометрии Римана рассмотреть самоорганизацию модулей дифференцировки с межмодульными 2D каналами, в замкнутом пространстве которых происходит направленный перенос морфогенов и волн дифференцировки.

В рассматриваемой модели точки являются центрами биоединиц и система точек изучается без учета их природы. В зависимости от масштабного уровня иерархии спирально-циклической самоорганизации такими единицами могут быть клетки и группы клеток. Плоский каркас в евклидовой геометрии заменяется каркасом на поверхности Клиффорда (К-поверхности) в эллиптической геометрии Римана [2]. В соответствии с выбранной симметрией движения самоорганизация модулей дифференцировки ведется поэтапно с помощью биоединиц, находящихся на минимальном расстоянии от нулевой точки. Биоединицы отстоят друг от друга на несколько периодов формируемого каркаса. С помощью системы точек на К-поверхности (К-система) находятся точки расположения биоединиц заданного уровня самоподобия. К-система переносится параллельно самой себе по спирали от периферии к центру и точки фиксируются в пределах треугольного контура от нулевой до n-го масштабного уровня иерархии. Оболочки биоединиц с пониженной размерностью обеспечивают принцип самоподобия и плотнейшую упаковку. Начиная с нулевой точки распространение каркаса в пространстве осуществляется присоединением к фиксированным узлам новых биоединиц. Реализация связей происходит по прямым на К-поверхности с периодом, значительно превышающим период каркаса. Это обеспечивает формирование модуля дифференцировки путем оконтурирования замкнутого и еще не заполненного биоединицами каркаса. Последующее заполнение вакантных узлов каркаса идет без существенных увеличений его линейных размеров. Алгоритм для компьютерного построения модельных модулей дифференцировки с помощью групп переноса , в результате которого на К-поверхности получается каркас с фиксированными центрами биоединиц, проводится по следующему правилу [1]:

где ; A_F, T_K - группы матриц вращения, индуцируемых в сечении F-группой внешней симметрии 6mmm и преобразованием К-поверхности, соответственно; r_K - радиус К-поверхности; k - количество лежащих на сечении К-поверхности точек. Формирование биоструктуры завершается заполнением вакантных узлов, иерархическим распределением 2D каналов по всему каркасу, оконтуриванием внешней формы и образованием общего 2D канала, назначением которого является направленный массо- и энергоинформационный переносы в масштабах всего биообъекта. Моноцентрическая самоорганизация организма подразумевает единое направление переноса морфогенов по всем иерархически распределенным 2D каналам и необходимо для осуществления стадии волнового формообразования органов. Нарушение морфогенеза является следствием отклонений в процессе дифференцировки и может быть представлено в предлагаемой модели как изменение иерархического расположения модулей дифференцировки, вызывающее ветвление 2D каналов без общей направленности переноса морфогенов. При последующей самоорганизации модулей дифференцировки иерархия 2D каналов не восстанавливается, биоструктура характеризуется отсутствием правильной циркуляции морфогенов и распространения волн дифференцировки). Предложенный геометрический подход может служить основой для построения конкретных моделей как спирально-циклической самоорганизации многоклеточных организмов, так и процесса дифференцировки в фило- и онтогенезе.

1. Turing, A.M. The chemical basis of morphogenesis. // Phil. Trans. Roy. Soc. London. Ser. B. 1952.- V. 237, P. 37-72.

2. Rudnev, S.V. Application of elleptic Riemannian geometry to problems crystallography. // Comp. Math. Applic. 1988, V. 16, P. 597-616.

3. Gordon, R.. The Hierarchical Genome and Differentiation Waves: Novel Unification of Development, Genetics and Evolution. –Singapore, World Scientific and London: Imperial College Press. 1999. - 1836 p.