|
Моделирование гидготермодинамического состояния приводного слоя Таганрогский государственный радиотехнический университет Научный руководитель: Куповых Геннадий Владимирович, Клово Александр Георгиевич, к.ф.-м.н. Специальные градиентные измерения метеорологических величин в приводном слое, проведенные в акватории Азовского моря в августе 2000 года, выявили существование устойчивой температурной инверсии в атмосфере вблизи поверхности воды масштабом порядка одного метра. Общая система уравнений описывающая гидротермодинамическое состояние нижних слоев атмосферы состоит из уравнения динамики, записанного для трех компонент скорости ветра (u, v, w), законов сохранения энергии и массы, уравнений состояния для влажного воздуха [1]. Для моделирования наблюдаемой температурной инверсии в приводном слое основные уравнения гидротермодинамики могут быть сведены к системе, состоящей из уравнений теплопроводности и переноса водяного пара в турбулентной атмосфере, а также уравнения состояния влажного воздуха:
В уравнениях использованы общепринятые в метеорологии обозначения физических величин [2]. Первые слагаемые в правых частях уравнений (1) и (2) характеризуют горизонтальный приток тепла (адвекцию), вторые слагаемые – конвективный перенос, третьи слагаемые – турбулентный приток тепла, четвертое слагаемое в уравнении (1) учитывает приток тепла, обусловленный переносом водяного пара. Анализ и решение системы уравнений (1)-(3) в трех и двумерных случаях предполагают применение аддитивных схем расщепления (на локально одномерную и локально двумерную схемы алгоритмов). При этом для численного решения одномерных и двумерных задач используются быстрые прямые и итерационные методы расчетов сеточных уравнений [3]. Для интерпретации полученных экспериментальных данных исходные уравнения (1)-(3) могут быть упрощены и сведены к одномерной нестационарной системе без учета адвективного и конвективного слогаемых. В этом случае система имеет вид
где Граничные условия
где Уравнение теплового баланса на поверхности воды имеет вид:
где В этом случае одномерная нестационарная модель приводного слоя позволила получить инверсное распределения температуры и влажности воздуха над водной поверхностью при задании соответствующих начальных и граничных условий. Работа выполнена при поддержке Американского Фонда Гражданских Исследований и Развития. Список публикаций: [1] Лайхтман Д.Л. Физика пограничного слоя атмосферы. Ленинград, Гидрометеоиздат, (1970). [2] Матвеев Л.Т. Курс общей метеорологии. Физика атмосферы. –Ленинград, Годрометеоиздат, (1984). [3] Клово А.Г., Куповых Г.В. Моделирование гидродинамических процессов в приводном слое атмосферы. Материалы Всероссийской научной конференции “Математическое моделирование в научных исследованиях”. Ч. II, Ставрополь, (2000). |
| (c) АСФ России, 2001 |
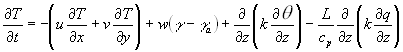 , (1)
, (1)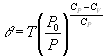 - потенциальная
температура,
- потенциальная
температура,