ВНКСФ7: Никитин Дмитрий Александрович: Моделирование перколяции в объектах с различной фрактальной размерностью

Моделирование перколяции в объектах с различной фрактальной размерностью

Никитин Дмитрий Александрович
Гродненский государственный университет

Научный руководитель: Лиопо Валерий Александрович, д.ф.-м.н., проф.
Соавторы: Белко Александр Владимирович

Работа посвящена вопросам моделирования структуры композитных систем с применением новых методов, базирующихся на теориях, активно развиваемых в последние 30 лет: теория перколяции, фрактальная геометрия. Применение аппарата этих теорий позволяет детализировать описание процессов, которое, часто, невозможно обеспечить традиционными методами (например, описание с помощью дифференциальных уравнений).

На начальном этапе решалась задача создания модельных объектов с фрактальной структурой и изучение их геометрических характеристик. На основе модели Виттена-Сандера была разработана программа , которая строит фрактальный кластер и определяет его фрактальную размерность. В ходе экспериментов была исследована зависимость фрактальной размерности кластера от размеров области генерации и места генерации начальной точки движения каждой частицы. Установлено, что при размерах области >140х140 ячеек фрактальная размерность не меняется (в пределах погрешности) и равна D=1.66± 0.03. В ходе проведенных численных экспериментов исследовалась также зависимость фрактальной размерности кластера от вероятности прилипания частицы к фрактальному кластеру и от взаимного расположения частицы и фрактального кластера. Рассмотрены четыре варианта взаимного расположения диффундирующей частицы и кластера (рис.1).

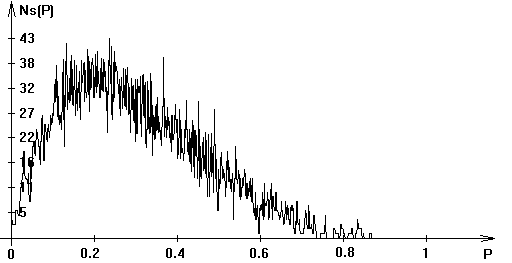
Рис.1

Присоединение к данному фрактальному кластеру осуществляется с некоторой вероятностью р1, р2, р3, р4 в зависимости от взаимного расположения диффундирующей частицы и кластера. Установлено, что при уменьшении вероятности прилипания р1 фрактальная размерность кластера увеличивается, при уменьшении вероятности р3 фрактальная размерность кластера уменьшается. Вариации значений вероятностей в вариантах 2 и 4 на фрактальную размерность кластера оказвают малое влияние. В результате проведенных исследований установлено, каким образом меняя значение вероятности прилипания для различных случаев можно получать фрактальные кластеры фрактальной размерности в пределах от 1.54 – 1.8.

Для определения характеристик и генерации перколяционных кластеров использовались выше описанные модели а также модель “случайного дождя”. Определялась зависимость функции распределения среднего размера кластера N_s от вероятности p (Рис. 2). В эксперименте размер кластера принимался равным 1. Размер решетки 20х20. Шаг изменения вероятности равнялся 0.001. Выполнялись 20 измерений для каждого значения вероятности.

Pис. 2

Средний размер кластера растет по мере приближения вероятности к пороговой. При наблюдается максимум, при дальнейшем увеличении вероятности, средний размер кластера уменьшается. Это объясняется тем, что все большая доля занятых ячеек принадлежит соединяющему кластеру, который исключается из распределения.

Перколяционный кластер является примером случайного статистического фрактала. Разработанная методика была применена для определения фрактальной размерности кластеров для вероятности заполнения в пределах от пороговой до . Данные показывают, что фрактальная размерность перколяционных кластеров не является постоянной величиной, и зависит от вероятности заполнения решётки.

В работе рассмотрены вопросы применения новых теорий (фрактальная геометрия, теория перколяции) для описания физических процессов и объектов.

Исследована численная модель генерации фрактальных структур по методу Виттена-Сандера. Установлены зависимости фрактальной размерности от размеров сетки генерации и способов генерации блуждающей ячейки. Составлена программа для генерации фрактальных структур. Исследованы фрактальные характеристики метода случайного блуждания.
Разработана компьютерная модель генерации перколяционных кластеров. На основе этой модели исследована пороговая проводимость композиционной системы. Показано, что перколяционные кластеры имеют фрактальную структуру. Получена зависимость сопротивления сетки от фрактальной размерности.
Разрабатываемые модели предполагается использовать для описания процессов переноса в композитных системах на основе полимеров с фрактальной структурой наполнителя.