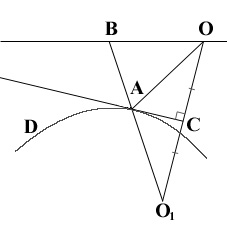
|
О единственности восстановления формы океанического дна по результатам измерений отраженных волн Санкт-Петербургский государственный университет Научный руководитель: Камоцкий Владимир Ильич, к.ф.-м.н. Рассматривается задача об определении неизвестной формы океанического дна, если в каждой точке на поверхности океана известно время пробега и, следовательно, расстояние, пройденное акустической волной, излучаемой из фиксированной точки на поверхности океана. Поместим начало декартовой системы координат в точку O, где расположен точечный источник акустических колебаний. Ось абсцисс направим по поверхности океана (см. рис. 1), ось аппликат - вглубь океана, а ось ординат - перпендикулярно этим осям.
рис. 1 Предположим, что зависимость глубины океана от координат описывается соотношением z = f(x,y). Пусть в каждой точке B на поверхности океана известна функция L(x,y), равная расстоянию OAB от источника, отсчитываемому вдоль луча. Предполагается, что отражение лучей от поверхности дна происходит по закону Снеллиуса. Будем считать, что дно таково (функция z=f(x,y) такова), что лучи отразившиеся от дна не могут второй раз отразиться от него и достигают либо поверхности океана, либо уходят на бесконечность. Кроме того, будем считать функцию L(x,y) однозначной и имеющей две непрерывные производные. Это означает, что в каждую точку приходит не более одного луча. Данное предположение выполняется по крайней мере для поверхностей не слишком отличающихся от плоскости. Для решения поставленной задачи вводится семейство специальных шестипараметрических поверхностей S. Это семейство является обобщением семейства кривых K, введенных в работе [1]. Основным свойством этих поверхностей является полиномиальная зависимость квадрата пройденного расстояния от координат M(x,y) = L2(x,y) = a0+a1x+a2y+a11x2+a12xy+a22y2 где a 0, a1 , a2 , a11 , a12, a22 - некоторые коэффициенты, определяемые по параметрам поверхности S. Несмотря на более сложное задание, чем обычные поверхности второго порядка, семейство S обладает рядом достоинств. В частности, более простыми получаются формулы, описывающие отражение от поверхности S.Искомая поверхность строится как огибающая семейства поверхностей S. Для этого вначале в каждой точке B определяется параметр R2 = M – Mxx - Myy + Mxxx2/2 + Mxyxy + Myyy2/2 (1) Геометрический смысл параметра
R(x,y) таков. Проведем в точке отражения A касательную плоскость к поверхности
дна и построим точку O1, симметричную точке O относительно этой плоскости. В
работе показано, что параметр R равен расстоянию ОO1 между точками. Теперь для
нахождения месторасположения точки A мы можем по трем сторонам L(x,y), R(x,y) и
rє Теорема. Пусть функция L(x,y)О С2, расстояния L(x,y), r и параметр R, полученный по формуле (1), связаны для всех x, y неравенствами треугольника. Тогда уравнение поверхности дна определяется однозначно. Отметим, что аналогично работе [1] можно восстанавливать неизвестную форму поверхности дна при помощи огибающей семейства эллипсоидов вращения. Этот подход позволяет доказать единственность донной поверхности при несколько отличных от сформулированных в теореме условиях. Полученные результаты можно использовать не только при исследовании океанического дна, но и при решении тех задач, где нужно восстановить профиль поверхности, зная отраженные волны. Например, подобные задачи возникают в ультразвуковой и рентгеновской дефектоскопии, при сейсмической разведке полезных ископаемых. Список публикаций: [1] И.А.Старков Определение профиля поверхности по результатам измерения отраженных волн. Аничковский вестник 2000, № 23, с. 41 –50. |
построить треугольник ОO1B. Восстановив срединный
перпендикуляр к стороне OO1 и найдя точку его пересечения со стороной BO, мы и
получим точку A на дне. Таким образом, точка A на дне однозначно определяется по
L(x,y), R(x,y) и r. В результате нами доказана теорема.| (c) АСФ России, 2001 |