МНОГОМЕРНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ЭЙНШТЕЙНА

Лосенкова Руслана Анатольевна

Научный руководитель: Шаров Г.С.,канд. физ.-мат. наук,доц. каф. функц.ан. и геом. ТвГУ

Тверской государственный университет, г.Тверь, Россия

В работе рассматриваются решения уравнений Эйнштейна шваршильдовского типа (центрально-симметричные решения в пустоте) для случая псевдоримановых многообразий различной размерности в присутствии — члена. Анализируются условия, при которых возможны решения типа черной дыры.

Вопрос о существовании и характере решений, описывающих черные дыры в гравитационных моделях с многообразиями нестандартной размерности , в настоящее время вызывает большой интерес [1,2,3]. В частности, работа [2] посвящена 2+1-мерным моделям с — членом (), работа [3] — случаю с .

В настоящей работе при различных значениях рассмотрены -мерные решения уравнений Эйнштейна

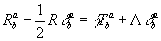(1)

шварцшильдовского типа, то есть обладающие свойством центральной симметрии решения этих уравнений в пустоте ( — материя отсутствует везде, кроме центра симметрии). Случаю , отвечает классическое решение Шварцшильда.

Будем искать стационарные решения уравнений (1) шварцшильдовского типа для многообразия размерности . Условие центральной симметричности означает, что если на сечении искомого многообразия гиперповерхностью const ввести радиальную координату и угловые координаты где то метрику исследуемого многообразия можно записать в виде:

Подставляя метрический тензор в уравнения Эйнштейна (1),

получим систему из уравнения:

…………………………………………………………………..

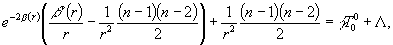
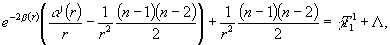
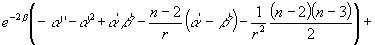
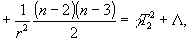
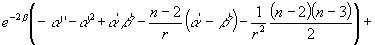
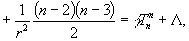
Их решение в случае имеет вид:

 

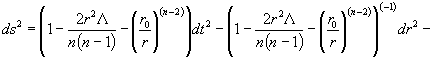
Найденные решения шваршильдовского типа исследованы с точки зрения описания черных дыр. Отметим, что в случае , возможны стационарные решения характеризуемые наличием двух различных горизонтов черной дыры.

Литература:

1. И.Д.Новиков, В.П.Фролов Физика черных дыр М.: Наука, 1986

2. M.Banados, M.Henneaux, C.Teitelboim, J.Zanelli Geometry of 2+1 black hole. Phys. Rev. D, V. 48, p.1506-1525, 1993.

3. К.А.Бронников, В.Н.Мельников О черных дырах в

многомерной гравитации //Итоги науки и техники. Сер. классическая теория поля и теория гравитации. ВИНИТИ 1992 с. 67-88

e-mail: asf@asf.e-burg.ru