МНОГОКРАТНАЯ ДИФРАКЦИЯ НА СЕРИИ ПОЛУЭКРАНОВ

Настаченко Алексей Семенович

Ростовский государственный университет, г. Ростов-на-Дону, Россия

Дифракция радиоволн на серии поглощающих полуплоскостей является одной из классических задач теории дифракции, имеющей важное прикладное значение, например, для прогнозирования напряженности поля УКВ в городе. Теоретическое решение задачи [1] не обеспечивает необходимые для прикладных расчетов устойчивость и скорость вычислений при большом количестве полуэкранов. Численно-аналитические методы [2,3] не дают эффективного аналитического решения для полуэкранов ограниченных поверхностью с малой кривизной. Рассмотрим решение, позволяющее установить связь множителя ослабления с кривизной ограничивающей поверхности без ограничений на количество полуэкранов.

При дифракции на произвольно расположенных по высоте ребрах полуэкранов множитель ослабления определяется n-кратным интегралом с различными нижними пределами. После замены переменных они равны нулю, а подынтегральная функция содержит безразмерные высоты ребер только в виде вторых конечных разностей. От них легко перейти к кривизне поверхности, если ее значение достаточно мало. Ограничимся случаем цилиндрической волны и нулевой высоты источника над ограничивающей поверхностью. Множитель ослабления принимает вид

,

,

, ,

,

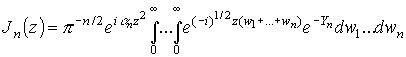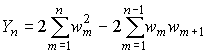l – длина волны, d – расстояние между поглощающими полуплоскостями, ym – высота ребра m-плоскости (y0=yn+1=0), n – количество полуэкранов. Для выявления физических закономерностей в нашей задаче введем безразмерный параметр

,

который связан с величиной z по формуле и не зависит от n, D=(n+1)d – расстояние между источником и точкой наблюдения. Отрицательные значения параметра r соответствуют выпуклой поверхности, положительные – вогнутой.

Опуская способ вычисления интеграла Jn(z), описанный в [4], приведем номограмму для нахождения модуля множителя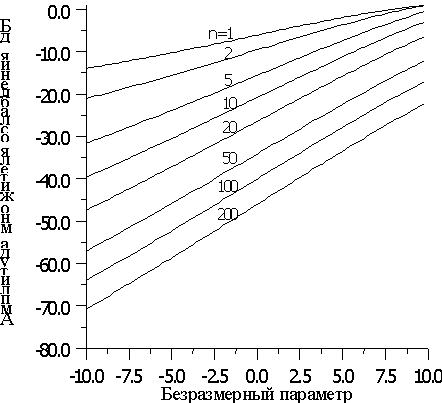 в виде, удобном для инженерного использования. При больших значениях n и небольших r множитель приближенно факторизуется , . Физически это означает, что уменьшение напряженности поля происходит вследствие увеличения роли двух факторов: кратности дифракции и затеняющего действия поверхностью.

Рис. Номограмма для нахождения множителя ослабления.

Выводы.

  1. При распространении волны под малыми углами скольжения над серией поглощающих полуэкранов, ребра которых образуют поверхность с малой кривизной, дифракционные потери зависят от кривизны поверхности, а не от высоты.
  2. Если кривизна поверхности мала и количество полуэкранов достаточно велико, то изменение напряженности поля с увеличением их числа практически не зависит от кривизны поверхности и расстояния. Множитель ослабления приближенно факторизуется.

Список литературы

  1. Vogler L.E. An attenuation function for multiple knife-edge diffraction. // Radio Sci., 1982, v.17, n.6, p.1541-1546.
  2. Piazzi L., Bertoni H.L. Effect of terrain on path loss in urban environments for wireless applications. // IEEE Trans. on Ant. and Propag., 1998, v.46, n.8, p.1138-1147.
  3. Tzaras C., Saunders S.R. Rapid, uniform computation of multiple knife-edge diffraction. // Electron. Lett., 1999, v.35, n.3, p.237-239.
  4. Nastachenko A.S. Analytical solution to diffraction problem in series of half-screens bounded by low-curvature surface. // Electron. Lett., 1999, v.35, n.22, p.1928-1929.

e-mail: asf@asf.e-burg.ru