 (1)
(1)Прямоугольный волновод с киральным включением
Костюк Л. Ю., Мещеряков В. А., Мудров А. Е.
Томский Государственный Университет, г.Томск, Россия
В замкнутой форме получены выражения для виртуальных токов, обусловленных наличием киральных включений в прямоугольном волноводе, в терминах которых формулируется задача о собственных электромагнитных волнах в регулярных направляющих структурах.
Материальные уравнения электродинамики для сред содержащих киральные объекты имеют вид [1]:
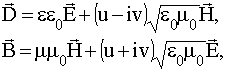 (1)
(1)
где ![]() ,
, ![]() , - магнитная и
диэлектрическая проницаемости,
, - магнитная и
диэлектрическая проницаемости, ![]() параметры невзаимности Теллегена и
киральности среды соответственно,
параметры невзаимности Теллегена и
киральности среды соответственно, ![]() . Нормированные
комплексные амплитуды векторов напряженности
электрического
. Нормированные
комплексные амплитуды векторов напряженности
электрического ![]() и
магнитного
и
магнитного ![]() полей с
учетом материальных соотношений [1] связанных
системой уравнений Максвелла можно записать в
следующем виде:
полей с
учетом материальных соотношений [1] связанных
системой уравнений Максвелла можно записать в
следующем виде:
![]() (2)
(2)
где ![]()
![]()
второе уравнение получается из
приведенного путем замены переменных со знаком
тильда на аналогичные, без
этого знака, и наоборот (здесь и далее по тексту
выполняется принцип перестановочной
двойственности). Наличие в правой части
уравнений так называемых виртуальных
электрического ![]() и
магнитного
и
магнитного ![]() токов
обусловлено включением в прямоугольный волновод
неоднородностей обладающих киральными
свойствами:
токов
обусловлено включением в прямоугольный волновод
неоднородностей обладающих киральными
свойствами:
![]() . (3)
. (3)
Решение системы уравнений (2) проведем
с использованием метода собственных волн [2].
Cобственные волны электрического и магнитного
типов для регулярных прямоугольных волноводов
представляют собой полную на поперечном сечении
волновода систему векторных функций [3], поэтому поперечные составляющие
электромагнитного поля в частично заполненном
волноводе можно представить в виде суперпозиции
поперечных составляющих поля в волноводе,
полностью заполненном средой с диэлектрической
и магнитной проницаемостью ![]() и
и ![]() :
:
![]() . (4)
. (4)
Подстановка поперечных составляющих электромагнитного поля (4) в систему уравнений (2) с учетом соотношений (3) приводит к выражениям полей в следующей форме:
![]() , (5)
, (5)
где векторы ![]() и
и ![]() суть
суперпозиции базисных функций с коэффициентами
суть
суперпозиции базисных функций с коэффициентами ![]() и
и ![]() для прямых и
обратных волн соответственно.
для прямых и
обратных волн соответственно.
Решая совместно уравнения (3) и (5), получим выражения для виртуальных токов:
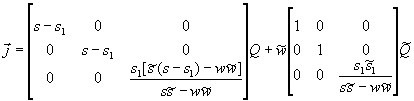 . (6)
. (6)
Соотношения (5) и условия ортогональности базисных функций позволяют спроектировать уравнения (2) на систему алгебраических уравнений относительно коэффициентов разложения:
![]() , (7)
, (7)
где ![]() - постоянная распространения p-й моды базисной волны,
- постоянная распространения p-й моды базисной волны, ![]() - норма волны,
- норма волны, ![]() - некоторый
параметр. Матрица коэффициентов системы с учетом
выражений для виртуальных токов (6) имеет вид:
- некоторый
параметр. Матрица коэффициентов системы с учетом
выражений для виртуальных токов (6) имеет вид:
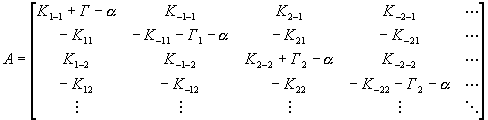 . (8)
. (8)
Система уравнений (7) относительно
параметра а может быть сформулирована в форме ![]() , то есть
приведена к задаче о полной проблеме на
собственные значения для матрицы
, то есть
приведена к задаче о полной проблеме на
собственные значения для матрицы ![]() . Причем
собственные вектора этой матрицы будут являться
наборами коэффициентов разложения поля частично
заполненного волновода а собственные значения
матрицы - постоянными распространения
собственных типов волн волновода с
неоднородностью.
. Причем
собственные вектора этой матрицы будут являться
наборами коэффициентов разложения поля частично
заполненного волновода а собственные значения
матрицы - постоянными распространения
собственных типов волн волновода с
неоднородностью.
Поскольку параметры среды на поперечном сечении зависят от координат, то интегрирование по поперечному сечению волновода сводится к интегрированию по каждой включенной неоднородности в отдельности и аддитивно учитывается при вычислении элементов матрицы.
e-mail: asf@asf.e-burg.ru