Движение твердой частицы под влиянием колебаний пузырька в сферичЕской колбе с жидкостью при воздействии акустического поля.

Болотнов Игорь Анатольевич

Научный руководитель: Ахатов Искандер Шаукатович, д.ф.-м.н., профессор, зав.каф. Механики сплош-ных сред математического факультета БашГУ

Башкирский Государственный Университет, г.Уфа, Россия.

Рассматривается движение твердой частицы, помещенной в сосуд с водой, в центре которого под действием акустического поля пульсирует воздушный пузырек.

Давление жидкости внутри сферической колбы, в которой сформирована стоячая акустическая сферическая волна, задается функцией [1]:

, (1)

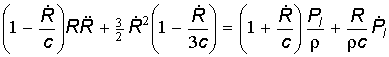где — расстояние от центра колбы, — круговая частота колебаний, — волновое число акустического поля, с — скорость звука в жидкости. Предполагается, что колебания радиуса газового пузырька описываются уравнением Херринга-Флина, справедливого в приближении слабосжимаемой жидкости [2]:

, (2)

в котором давление жидкости на границе с пузырьком задается выражением

,

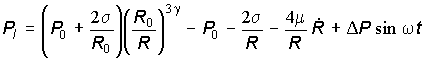где R, — текущий и начальный радиус пузырька, — плотность жидкости, — коэффициент поверхностного натяжения, — вязкость жидкости, — показатель адиабаты совершенного газа.

Запишем уравнение движения частицы, учитывая действующие на нее силы: тяжести, Архимеда, Бьеркнеса, присоединенной массы и вязкого сопротивления. Слагаемые, соответствующие этим силам, расположены в правой части уравнения (3) в указанной последовательности:

, (3)

где —радиус частицы (шарика), — ее объем, — скорость частицы, — скорость жидкости около частицы.

Скорость жидкости зависит от сформированной сферической волны и радиальных колебаний пузырька. Используем следующее выражение для скорости жидкости:

,

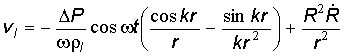которое получается исходя из уравнений сохранения массы, импульса, уравнения состояния для слабосжимаемой жидкости и уравнения (1).

Так как задача является осесимметричной, представим уравнение (3) в полярной системе координат (r,):

: = ;

: = . (4)

Учитывая уравнение Херринга-Флина (2) для нахождения радиуса пузырька R и уравнения (4) для определения координат частицы r и получим замкнутую систему трех обыкновенных дифференциальных уравнений второго порядка, которая численно решалась методом Дормана-Принса [3].

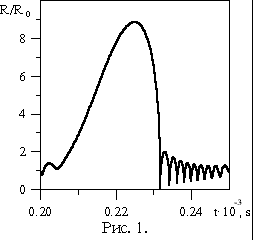
На рис. 1. показан один цикл периодических колебаний радиуса пузырька при R0=10-5 , =20 кГц, P0 = 105 Па, Па.

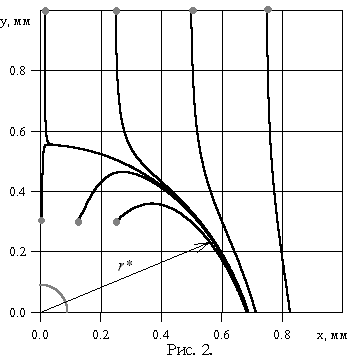
На рис. 2 показаны траектории движения шарика (сплошные линии) при различных начальных координатах, помеченных кружочками. Колеблющийся пузырек находится в начале координат. Расчеты проводились для шарика с плотностью =2? 103 кг/м3 и радиусом =10-5 м. Траектории шарика огибают колеблющийся пузырек на расстоянии r*=0.55 мм. Эта величина в 7 раз превышает максимальный радиус колеблющегося пузырька. Расчеты были проведены также для различных радиусов шарика при сохранении той же плотности и начальных координат. При увеличении радиуса шарика его траектория не изменяется, а растет скорость движения. При уменьшении плотности шарика с сохранением начального радиуса его траектория удаляется от пузырька на большее расстояние. Таким образом, радиус сферы, окружающей пузырек, куда не может проникнуть твердый шарик, увеличивается при уменьшении плотности шарика и не зависит от его радиуса. Эти выводы справедливы для постоянного начального радиуса колеблющегося пузырька и неизменного внешнего периодического воздействия.

Литература

  1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988.
  2. Маргулис М.А. Основы звукохимии. М.: Мир, 1984.
  3. Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. М.: Мир, 1990.

e-mail: asf@asf.e-burg.ru