ТРАНСЛЯЦИОННОЕ ДВИЖЕНИЕ КАВИТАЦИОННОГО ПУЗЫРЬКА В АКУСТИЧЕСКОМ ПОЛЕ
Калякина Ольга Леонидовна
Научный руководитель: хатов Искандер Шаукатович, д.ф.-м.н., профессор, зав.лаб. ИМех УНЦ РАН
Институт Механики УНЦ РАН
, г. Уфа, РоссияДинамика кавитационного пузырька включает как радиальные колебания, так и трансляционное движение, т.е. перемещение пузырька в пространстве. Трансляционное движение пузырька в акустическом поле индуцируется функцией давления, зависящей от временной и пространственной переменных. Изменение давления по пространственной переменной действует на поверхность пузырька, а зависимость давления от времени вызывает его радиальные колебания, которые изменяют объём пузырька и приводят к перемещению пузырька в пространстве.
В качестве физической модели рассматривается сферическая колба, наполненная жидкостью, находящейся под действием акустического поля, заданного в виде сферической стоячей волны
|
где 
акустическое давление в центре
сферической колбы с амплитудой 
, 
- радиальная координата, 
-
частота, 
- волновое число акустического поля:
, 
- длина волны, 
-
скорость звука в жидкости.
Движение пузырька рассматривается в полярных координатах
,
где
- расстояние от пузырька до центра
колбы, 
- угол отклонения от вертикальной
оси.
В физической постановке задаче принимаются во внимание следующие силы, действующие на пузырек.
1.Выталкивающая сила:
|
Здесь
- объем пузырька
,
- радиус
пузырька, 
- плотность жидкости, 
-
плотность газа.
2. Сила Бьеркнеса: сила, действующая на колеблющийся пузырёк в поле стоячей звуковой волны,
|
3. Силу присоединенной массы: движущийся пузырёк генерирует некоторую инерцию, значительная доля которой приходится на инерцию жидкости, окружающей пузырёк
|
4. Сила сопротивления жидкости. В рамках Стоксовой аппроксимации известно решение Адамара-Рыбчинского, использование которой даёт следующую формулу силы, действующей на движущийся в жидкости пузырёк
|
5. Будем считать, что масса пузырька равна
|
На основе принятых выше предположений построена модель из трех ОДУ второго порядка:
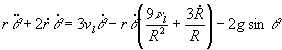
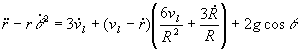
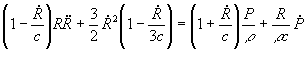
2. Результаты
численных экспериментов
Полученная модель исследована численным методом Дормана-Принса пятого порядка точности, которая позволяет автоматически подбирать длину шага так, чтобы локальная погрешность не превышала предписанной допустимой величины.
В ходе численных экспериментов было выявлено существование трёх видов решений исследуемой системы уравнений. Тип решения зависит от величины начального радиуса пузырька
. При 
мкм, (
мкм),
радиальная координата 
имеет периодический
характер с амплитудой около 500 mn. При 
мкм, радиальная координата имеет
хаотический характер. При 
мкм радиальная
координата имеет квазистационарный характер.
e-mail: asf@asf.e-burg.ru
.
.
.
.